Eine Multiplikation gleicher Faktoren kann als Potenz geschrieben werden:

Ist die Basis positiv, ist auch jede Potenz positiv; ist die Basis negativ, so ist jede Potenz mit geradem Exponenten positiv und jede Potenz mit ungeradem Exponenten negativ.
Die Quadratwurzel √ a einer positiven Zahl a ist diejenige Zahl, die mit sich selbst multipliziert a ergibt:
√ a . √ a = (√a)² = a

Beispiel: Gib jeweils den Wert der Potenz an.

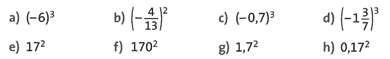
Lösung :

Beispiel: Gib jeweils den Wert der Quadratwurzel an.

a) √ 81
b) √ 225
c) √ 3600
d) √ 1,96
e) √ 1960 000
f) √ 2,89
g) √ 0,000 289
h) √ 625/169

Lösung :
a) 9; b) 15; c) 60; d) 1,4; e) 1400; f) 1,7; g) 0,017; h) 25/13

Beispiel: Welches Volumen hat ein Würfel mit der Kantenlänge 5 cm?
Lösung :
Er hat das Volumen 5³ cm³ = 125 cm³

Beispiel: Wie lang ist eine Seite eines Quadrats mit 225 m² Flächeninhalt?
Lösung :
Eine Seite misst √225 m = 15 m.