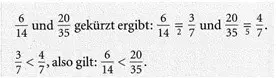Herr Dörnfeld hat für seine Söhne eine Pizza mitgebracht. Moritz, der ältere Sohn, soll 2/3 und Felix 4/12 davon erhalten. Moritz fühlt sich ungerecht behandelt. «Dazu besteht überhaupt kein Grund», sagt sein Vater und erklärt ihm:
«Wenn du 2/3 und 4/12 miteinander vergleichst, wirst du wissen, warum. Bringe zunächst die beiden Brüche auf den gleichen Nenner (mache sie gleichnamig).»
Um Brüche miteinander vergleichen zu können, müssen sie einen gemeinsamen Nenner haben. Den gemeinsamen Nenner erhältst du durch Erweitern oder durch Kürzen.
Brüche vergleichen durch Erweitern auf einen gemeinsamen Nenner:
Hinweis : Beim Erweitern wird multipliziert, beim Kürzen dividiert.
Beispiel 1: Brüche vergleichen durch Kürzen auf einen gemeinsamen Nenner:
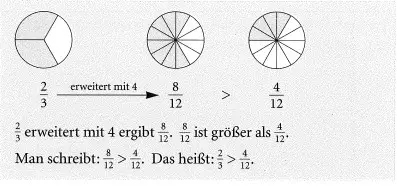
Beispiel 2:
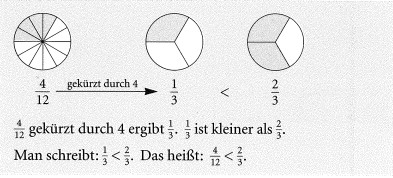
Hinweis : Kürzen heibt, Zahler und Nenner durch dieselbe Zahl dividieren.
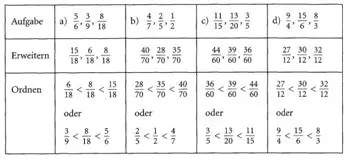
Übung 1: Ordne die Brüche der Größe nach. Beginne mit dem kleinsten.
Lösung 1:
![]()
Beispiel 3:
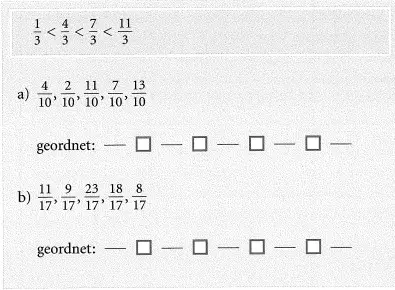
Hinweis : “<” heibt “kleiner als”, “>” heibt “gröber als” Die Spitze zeigt immer auf die kleinere Zahl. Überprüfe nun deine Lösungen.
Übung 2: Erweitere die Brüche auf einen gleichen Nenner. Entscheide dann, welcher Bruch der kleinere ist.
Beispeil 4: Ist der kleinere Nennet im gröberen enthalten, wird der Bruch mit dem kleineren Nenner etsprechend erweitert.
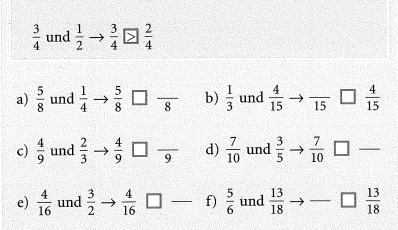
Überprüfe die Übung mit Hilfe des Lösungsteils.
Um 2/3 und 3/4 der Größe nach vergleichen zu können, müssen wir die Brüche so erweitern, dass die Nenner gleich groß sind.
Lösung 2:
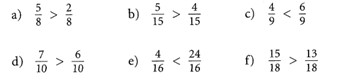
Übung 3: Berechne die Aufgaben aund b. «Gleichnamig machen» bedeutet
«auf einen gemeinsamen Nenner bringen».

So findest du leicht einen gemeinsamen Nenner: Vervielfache den größeren Nenner so oft, bis der kleinere Nenner in ihm enthalten ist.

Lösung 3:

Übung 4: Setze die Zeichen «<» oder «>» ein.

Lösung 4:
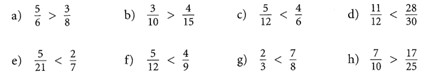
Übung 5: Ordne die folgenden Brüche der Größe nach. Beginne mit dem kleinsten.
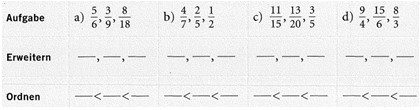
Hinweis : Brüche können auch verglichen werden, indem man sie auf einen gemeinsamen Nenner kürzt.
Beispeil : Dieses Verfahren lässt sich allerdings nur selten anwenden.