Die Spiegelzahlen geben dir eine Möglichkeit, negative Zahlen graphisch zu addieren. Betrachte das Beispiel

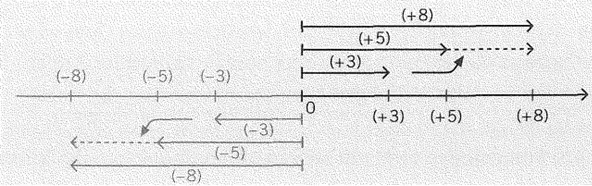
Positive und negative Zahlen werden durch Pfeile dargestellt. Die Pfeillänge gibt den Abstand der Zahl von 0 an.

Der Abstand einer rationalen Zahl x von 0 wird Betrag dieser Zahl x genannt.

Beispiel
|(—3)| = 3, denn (-3) hat den Abstand 3 von 0.
|(+5)| = 5, denn (+5) hat den Abstand 5 von 0.

Abstände sind immer positiv. Die Klammern können deshalb entfallen.

Du erkennst folgende Eigenschaften:
1.Der Betrag irgendeiner rationalen Zahl, die nicht 0 ist, muss positiv sein.
2.Der Betrag der Zahl Null ist 0.
3.Die Beträge von Zahl und Spiegelzahl sind gleich.

Übung 25
Bestimme die Spiegelzahlen und ihre Beträge.

Lösung 25

Die Pfeillänge einer Zahl in der Abbildung auf Seite 31 wird also durch ihren Betrag dargestellt. Mit der Richtung des Pfeils wird angegeben, ob die Zahl positiv oder negativ ist. Positive Zahlen sind wie die Zahlenachse gerichtet. Du erkennst aus der Abbildung: Die Addition (+3) + (+5) erfolgt so, dass der Pfeil für den einen Summanden (+3) mit seinem Anfangspunkt auf die Spitze des zweiten Summanden (+5) gesetzt wird. Die Spitze des Pfeils zeigt dann auf die Summe (+8).

Übung 26
Zeichne eine geeignete Zahlenachse. Prüfe die Behauptung, dass du im Beispiel auf Seite 31 dasselbe Resultat erhältst, wenn du den Pfeil für den Summanden (+5) an die Spitze des Summanden (+3) setzt.

Wenn du das Verfahren auf die Spiegelzahlen von (+ 3) und (+ 5) überträgst, stellst du fest, dass sich als Summe (-8) ergibt. Du könntest schreiben: (-3) + (-5) = (-8). Auch hier spielt es keine Rolle, welche Zahl du als ersten Summanden auswählst.
Für negative Zahlen legen wir deshalb fest:
Die Summe zweier negativer Zahlen ist eine negative Zahl. Der Betrag dieser Zahl ist die Summe aus den Beträgen der zwei Summanden.
Biespiel

Addiere nun positive und negative Zahlen. Betrachte dazu die Abbildung.

Wieder wird der Anfangspunkt des Pfeils für den zweiten Summanden (-3) an die Spitze des ersten Summanden (+8) gesetzt, jetzt aber in umgekehrter Richtung. Es ergibt sich die Spitze des Pfeils für (+5). Es ist also sinnvoll festzulegen: (+8) + (-3) = (+5)

Lösung:

Übung 27
Bestimme die Summen auf graphischem Wege mit Hilfe einer geeigneten Zahlenachse.
a) (-3) + (+8)
b) (-5) + (+3)
c) (-5) + (+5)

Lösung:

Biespiel

Die SOLL-Werte betragen insgesamt 1350,00 DM. Um den neuen Kontostand zu ermitteln, sind SO LL- und HABEN-Werte addiert worden: Positive und negative Zahlen wurden ohne Zuhilfenahme von Pfeil bildern addiert. (+8500) + (-1350) = (+7150)

Übung 28
Berechne den neuen Kontostand.

Lösung:
SOLL-Wert                                          : DM 1000,00
Addition der HABEN-Werte         : DM 850,00
Rest-SOLL                                            : DM 150,00 (DM 1000,00 – DM 850,00)
Neuer Kontostand                          : DM 150,00 SOLL

Für die Addition positiver und negativer Zahlen gilt die folgende
Addition von positiven und negativen Zahlen:
Subtrahiere vom größeren Betrag den kleineren und setze vor die Differenz das Vorzeichen der Zahl mit dem größeren Betrag.

Biespiel

Bei der Addition von (-13,8) und (-0,5)sind beide Summanden negativ. Die Beträge sind 13,8 und 0,5, ihre Summe ist 14,3. Das gemeinsame Vorzeichen ist ein Minuszeichen. (-13,8) + (-0,5) = (-14,3)

Bei der Addition von (-12,21) und (+2,3) haben die Summanden ein unterschiedliches Vorzeichen. Der größere Betrag ist 12,21, der kleinere 2,3. Die Differenz der Beträge ist 9,91. Der Summand mit dem größeren Betrag hat als Vorzeichen ein Minuszeichen. (-12,21)+ (+2,3) = (-9,91)

Übung 29
Addiere
Tipp: Zweifach periodische Dezimalbrüche werden mit dem Nenner 99 umgeformt.
a) (-4,28)+ (+5,16)
b) (+8,3) + (-8,3)
c) 0 + (-3)
d) (+13,089) + (-101,101)
e) (+12) + (-12,13)

Lösung:

Unterscheide bei der Addition rationaler Zahlen die folgenden Fälle.
Die Summanden können beide positiv oder beide negativ sein, oder sie können ein unterschiedliches Vorzeichen haben.
Die Tabelle auf Seite 36 zeigt dir, wie du jeweils addierst.

Additionstabelle für rationale Zahlen

Übung 30
Berechne die folgenden Summen. Lies zu Teilaufgabe e) vorher den nachfolgenden Tipp.

Tipp: Die Berechnung der Summe in Teilaufgabe e) der Übung 30 ist etwas schwieriger. Betrachte deshalb diese Hilfe:

Mit diesem Zwischenergebnis kannst du Teilaufgabe e) berechnen.

Lösung:

Übung 31
Berechne und vergleiche.
a) (-3) + (+5) und (+5) + (-3)
b) (-8) + (-1) und (-1) + (-8)
c) (+11,123) + (-11,234) und (-11,234) + (+11,123)

Lösung:
a) (-3) + (+5) = (+2); (+5) + (-3) = (+2)

1. b) (-8) + (-1) = (-1) + (-8) = (-9)
2. c) (+11,123) + (-11,234) = (-11,234) + (+11,123) = (-0,111)

Übung 31 zeigt, dass du die Reihenfolge der Summanden in einer Summe vertauschen kannst, ohne dass sich die Summe ändert. Schon auf Seite 33 hast du dieses Ergebnis erhalten. Es ist dir von früher als wichtige Eigenschaft der Addition von Bruchzahlen bekannt. Dieses Gesetz gilt auch für negative, allgemein für rationale Zahlen.

Kommutativgesetz der Addition Für alle rationalen Zahlen x und y gilt:
x+y=y+x
Bei der Addition rationaler Zahlen können die Summanden vertauscht werden.

Mit dem Kommutativgesetz ist eine Eigenschaft der Addition von Bruchzahlen auf die neue Zahlenmenge der rationalen Zahlen erweitert worden. Dieses mathematische Erweiterungsprinzip wird später zum Beispiel bei der Multiplikation wieder beachtet. Bisher hast du Summen aus zwei Summanden berechnet.
Du lernst nun, wie mehr als zwei Summanden addiert werden.