Ein wichtiger Spezialfall mehrgliedriger Produkte liegt vor, wenn alle n Faktoren x untereinander gleich sind. Solche Produkte werden Potenzen, genannt und mit xn bezeichnet.
Beispiel:
(+7) (+7) (+7) = (+343) = (+7)3
Du weißt von früher, dass die Zahl (+ 7) die Basis und 3 der Exponent dieser Potenz sind. Der Exponent gibt an, wie oft die Basis als Faktor auftritt.
Beispiel:
(-2) (-2) (-2) (-2) = (+16) = (-2)4
(-2)(-2)(-2)(-2)(-2) = (-32) = (-2)5
Wenn das Produkt x • x • x… • x eine gerade Anzahl von Faktoren hat, dann ist es nicht negativ, d. h. xn 0, wenn n gerade ist. Dieses Produkt wird nur dann 0, wenn x selbst 0 ist.
Potenzen mit geradem Exponenten sind nicht negativ.
Wenn das Produkt eine ungerade Anzahl von negativen Faktoren hat, dann ist es negativ, d. h. xn < 0, wenn n ungerade und x < 0 ist.
Potenzen mit negativer Basis und ungeradem Exponenten sind negativ.
Übung:Schreibe die folgenden Produkte als Potenzen. Berechne die Potenzen.
a) (-3)(-3)(-3)(-3)(-3) b) (+4)(+4)(+4)
c) (-1)(-1) (-1)(-1)(-1)(-1) d) (-0,5)(-0,5) (-0,5)(-0,5)
Lösung:
a) = (-3)5 = (-243) b) = (+4)3 = (+64) c) = (-1)6 = (+1)
Übung:Berechne die folgenden Potenzen.
a) (- 1,1 )3 b) (-1)8 c) (-3)3 d) (-17)2 e) [(-3) + (+8)]2
Lösung:a) (-1,331) b) (+1) c) (-27) d) (+289) e) (-3)+ (+8) = (+5); (+5)2 = (+25)
Klammcrinhalte werden zuerst berechnet. Ineinander geschachtelte Klammern berechnest du «von innen nach außen». Dabei geht Potenzieren vor «Punkt»-Rechnung und «Punkt»-Rechnung wiederum vor «Strich»-Rechnung.
Beispiel:
(+1,1) [(-1,2) + (+3)] (-1,8) – (-2,3)2(-2,4)
= (+1,1) (+1,8) (-1,8) – (+5,29) (-2,4)
= (+1,1) (-3,24)-(-12,696)
= (-3,564) – (-12,696)
= (+9,132)
Beispiel:
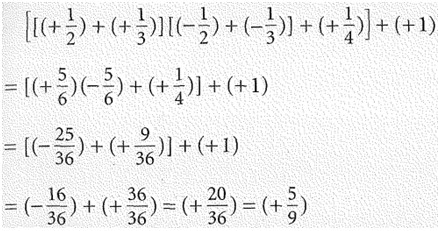
Übung:
Berechne wie im Beispiel.
a) [(+1,83) (-1,2) + (-0,51) (-2,5)] (-1,5)
b) [(-4,3) – (-2,8)] (-1) + (—2)(—3)3
c) [(—1)(+3,1) + (-2)] [(-2)2 + (-1)8] + (-8)
Lösung:
a) = [(-2,196) + (+1,275)] (-1,5) = (-0,921) (-1,5) = (+1,3815)
b) = (-1,5)(-1) + (-2) (-27) = (+1,5) + (+54) = (+55,5)
c) = [(-3,1) + (-2.)] [(+4) + (+1)] + (-8) = (-5,1)(+5) + (-8) = (-33,5)
Übung:Berechne wie im Beispiel.
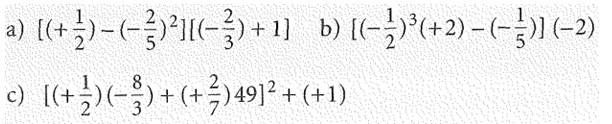
Lösung:
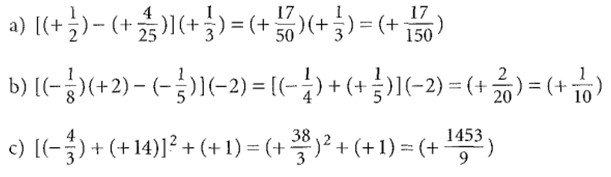

Besonders einfach berechnest du Potenzen, wenn die Basis (+1) oder (-1) ist. Wähle dir selbst eine natürliche Zahl n > 0. Du stellst fest: (+ l)n = (+1).

Übung:Berechne .
a) (-1,82)3(+0,75) b) (-0,5)3(+0,3)3(-1)
c) (+l,13)(-0,2)5 d) [(-0,5)(+ 0,3)]3(-1 )
Lösung:
a) = (-6,028568) (+0,75) = (-4,521426)
b) = (-0,125) (+0,027) (-1) = (+0,003375)
c) = (+1,13) (-0,00032) = (-0,0003616)
d) = (—0,15)3(—1) = (+0,003375)
Eine weitere Anwendung der Potenzen findest du bei den Zehnerpotenzen.
Beispiel:
10 = 101
100 = 10 • 10 = 102
1000 = 10 • 10 • 10 = 103
Die Bezeichnung Zehnerpotenzen für die Zahlen 10,100,1000 usw. auf Seite 15 ist nun verständlich. Der Exponent der Basis 10 gibt die Anzahl der Nullen an.