Rechengesetze und Klammern haben vor allem die Aufgabe, dire inen Überbilck zu verchaffen und eine Systematik in große Rechenaufgaben zu bringen. Bei Aufgaben mit vielen verschiedenen Rechenarten ist dies ein absolutes Muss.
Die 4 wichtigsten Regeln bei den Grundrechenarten:
1. Punktrechnung kommt vor Strichrechnung. (Punkt vor Strich)
Punktrechnungen sind Multiplikation (.) und Division (:),
Strichrechnungen sind Addition (+) und Subtraktion (-).
2. Alle Rechenausdrücke, die in Klammern stehen, werden zuerst berechnet.
3. Kommen in einem Rechenausdruck mehrere Klammern vor, so werden diese von inen nach außen berechnet, die innerste Klammer zuerst.
4. Kommen Klammer, Punktrechnung und Strichrechnung zusammen, so gilt die so genannte KlaPS-Regel (Klammer geht vor Punktrechnung und vor Strichrechnung).
Beispeile:
1. 2+3.4 = 2+12 = 14 Punkt vor Strich
2. 54 – (45-21) = 54-24 = 30 Klammer zuerst berechnen.
3. 34+[12-(5-3)] = 34+[12-2] Innerste Klammer zuerst berechnen.
= 34 + 10
= 44
4. 3.(34:2+3)-5 = 3.(17+3)-5
= 3.20-5
= 60-5
= 55
KlaPS-Regel : Klammer vor Punkt- und Strichrechnung. In der Klammer: Punkt vor Strich Hier gilt wieder Punkt vor Strich.
5. “Klammer-Champions-League”
{[(4-3).4-2].5}:2+7.3:(10-3)={[1.4-2].5}:2+21:7
= {2.5}:2+3
= 10:2+3
=5+3
=8
Neben den genannten Regeln gelten noch folgende 3 wichtige Gesetze. Diese gelten aber nur für bestimmte Grundrechenarten.
Kommutativgesetz (Vertauschungsgesetz):
• Bei der Addition : a+b=b+a
• Bei der Multiplikation : a.b=b.a
1. 3+8 = 8+3
11=11
(Stimmt!)
Bei einer Addition darf man die Summanden vertauschen.
2. 4.5 = 5.4
20 = 20
(Stimmt!)
Bei einer Multiplikation darf man die Faktoren vertauschen.
3. 12-4=4-12
Bei einer Subtraktion gilt diese Regel nicht.
4. 8:4=4:8
Bei einer Division gilt diese Regel nicht.
Assoziativgesetz (Verbindungsgesetz):
• Bei der Addition: (a+b)+c = a+(b+c)
• Bei der Multiplikation: (a.b).c = a.(b.c)
Achtung: Dieses Gesetz gilt nicht bei der Subtraktion und Division!
1. (12+4)+8 = 12+(4+8)
16+8 = 12+12
24 = 24
(Stimmt!)
Bei einer Addition darf man die Klammern beliebig setzen.
2. (3.4).7 = 3.(4.7)
12.7 = 3.28
84 = 84
(Stimmt!)
Bei einer Multiplikation darf man die Klammern beliebig setzen.
3. (14-7)-2 = 14-(7-2)
7-2 = 14-5
5 = 9
Bei einer Subtraktion gilt diese Regel nicht.
4. (60:6):3 = 60:(6:3)
10:3 = 60:2
3 Rest 1 = 30
Bei einer Division gilt diese Regel nicht.
Distributivgesetz (Verteilungsgesetz):
(a+b).c = a.c+b.c und (a-b).c = a.c-b.c
(a+b):c = a:c+b:c und (a-b):c = a:c-b:c
Dieses Gestz verwendet man meistens zum Ausklammern, Ausmultiplizieren und Ausdividieren.
Beispiele
1. 7.5+7.3=7.(5+3)=7.8=56 Kommt ein Faktor in einer Summe öfter vor, so kann man ihn ausklammern.
2. 8.3-2.3=(8-2).3=6.3=18 Kommt ein Faktor in einer Differenz öfter vor, so kann man ihn ausklammern.
3. 4.(2+1)=4.2+4.1
= 8+4
= 12 Ausmultiplizieren (das Gegenteil des Ausklammerns)
4. (128-96):32 = 128:32-96:32
= 4-3
= 1 Ausdividieren

69. Rechne vorteilhaft, indem du die Rechengesetze anwendest.
a) 17+19+83
b) 24:2+8:2
c) 29+(21+47)
d) (452+407)+593
e) (3.25).4
f) (70-4).3
g) 3.(40+8)
h) 2.(25.7)
i) 28+34+72+66
j) 375+39+125+61

69. Lösungen :
a) 17+19+83 = 17+83+19 = 100+19 = 119 Anwendung des Kommutativgesetzes
b) 24:2+8:2 = (24+8) : 2 = 32:2 =16 Anwendung des Distributivgesetzes
c) 29+(21+47) = (29+21) + 47 = 50+47 = 97 Anwendung des Assoziativgesetzes
d) (452+407)+593 = 452 + (407+593)
= 452 + 1 000
= 1 452 Anwendung des Assoziativgesetzes
e) (3.25).4 = (3.25).4 = 3.(25.4) = 3.100 = 300 Anwendung des Assoziativgesetzes
f) (70-4).3 = 70.3-4.3 = 210-12 = 198 Anwendung des Distributivgesetzes
g) 3.(40+8) = 3.40 + 3.8 = 120+24 = 144 Anwendung des Distributivgesetzes
h) 2.(25.7) = (2.25).7 = 50.7 = 350 Anwendung des Assoziativgesetzes
i) 28+34+72+66 = 28+72+34+66
=100+100
= 200 Anwendung des Kommutativgesetzes
j) 375+39+125+61 = 375+125+39+61
=500+100
=600 Anwendung des Kommutativgesetzes

70. Berechne den Wert der folgenden Rechenausdrücke.
a) [34-(23-12)]+4
b) (67-12).7+50:(35-25)
c) 2+5.3-8:2
d) 4+7.(25:5-5)+12:4
e) 39-(23-12)-18
f) (56-47)-(89-81)
70. Lösungen :
a) [34-(23-12)]+4 = [34-11]+4 = 23+4=27 innere Klammer vor äußerer Klammer
b) (67-12).7+50:(35-25) = 55.7+50:10
= 385+5
= 390 Klammern zuerst, Punkt vor Strich
c) 2+5.3-8:2 = 2+15-4=13 Punkt vor Strich
d) 4+7.(25:5-5)+12:4 = 4+7.(5-5)+3
= 4+7.0+3
= 4+0+3
= 7 Klammer zuerst
e) 39-(23-12)-18 = 39-11-18 = 28-18 = 10 Klammer zuerst
f) (56-47)-(89-81) =9-8=1 Klammer zuerst

71. Trage in die Kästchen die fehlenden Rechenzeichen so ein, dass die Gleichungen stimmen. Ergänze auch klammern, falls es nötig ist.

71. Lösungen :

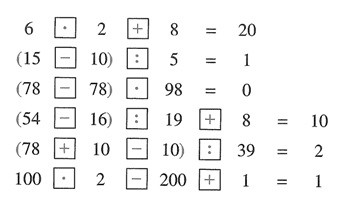
72. Berechne geschickt.
a) 80-45-25-10
b) 150-20+70-45-55
c) 856-34+99-666+45
d) 128-75+12-48+11-28
72. Lösungen :
a) 80-45-25-10 = 80-70-10=80-80=0
b) 150-20+70-45-55 = 150+50-100
= 200-100
= 100
c) 856-34+99-666+45 = 856+99+45-34-666
= 856+144-700
= 1 000 – 700
= 300
d) 128-75+12-48+11-28 = 128 4 11 + 12 – 75 – 48 – 28
= 128+23-75-76
= 151-151
=0