Die Stadt Mannheim wird auch Qua dratestadt genannt, denn es werden innerhalb der Stadtquadrate keine Straßennamen benötigt. Kombinatio nen aus Buchstaben und Ziffern genügen, um bestimmte Quadrate zu kennzeichnen, etwa A3 oder C4.

Die Kennzeichnung erfolgt ähnlich wie bei dem bekannten Schülerspiel „Schiffe versenken“. Du kannst damit eindeutig einen genauen Ort bestimmen.

In der Geometrie verwendet man Punkte und Linien zur genauen Kennzeichnung. Das Quadratgitter besteht aus einer waagrechten x-Achse und einer senkrechten y-Achse. Alle benachbarten Gitterlinien haben den gleichen Abstand voneinander. Die Ausdrücke Quadratgitter, Achsenkreuz, Koordinatensystem und Gitternetz werden oft gleichbedeutend verwendet.

1. Zeichne die Punkte A(2|3) und B(3|2) in ein geeignetes Quadratgitter.

Lösung:

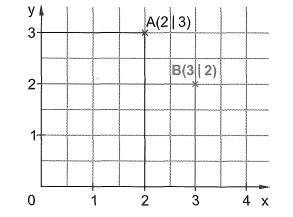
Achtung : Verwechsle nicht Punkte mit vertauschten Rechts- und Hochwerten.

2. Wie heißen die Koordinaten der Punkte im Quadratgitter?

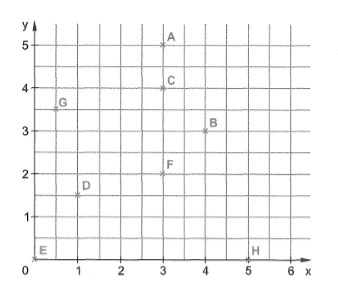
Lösung:

Die Koordinaten der Punkte lauten:

A(3|5), B(4|3), C(3|4), D(1|1,5), E(0|0), F(3|2), G(0,5|3,5), H(5|0)

3. Zeichne folgende Punkte in ein Quadratgitter ein und verbinde sie.
a) (2|2) B(5|3) C(3,5|5,5) D(0|6) E(4,5|0)
b) Wie groß muss das Quadratgitter sein, damit alle Punkte eingetragen werden können?
c) Wie viele Verbindungslinien zwischen den Punkten entstehen?

Lösung :

a)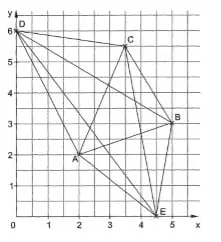

b) Das Gitter muss mindestens 5 cm x 6 cm groß sein.
c) Es entstehen 10 Verbindungslinien.
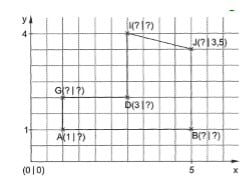
149 – Bestimme die fehlenden Koordinatenangaben.
Lösung :

150 – Zeichne die Punkte A(3|5), B(2|7), C(6|7) und D(4|8).
Vertausche Rechts- und Hochwerte und zeichne die entstandenen Punkte erneut. Zeichne alle möglichen Verbindungen zwischen den 8 Punkten ein.

Lösung:

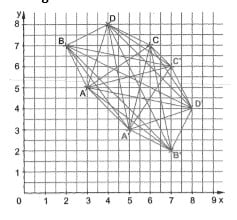
Das Einzeichnen der Rechts- und Hochwerte wird dir wahrscheinlich nicht schwerfallen. Beim Verbinden aller Punkte musst du eine gewisse Systematik anwenden, damit keine Linie vergessen wird. Am besten, du verbindest nacheinander jeden der Punkte mit allen anderen Punkten.

151 – Suche die Fehler in der Lösung zu folgender Aufgabe:
Zeichne die Punkte A(l,5|3), B(2,5|2,5), C(2|1,5), D(3,5|4,5), E(0|5), F(6|2) und G(5|4,5) in ein Quadratgitter und verbinde A, B und C und D, E, F und G.
Lösung:
Fehler:
1. Fehler: Der Punkt A heißt A(l,5|3) und eingezeichnet ist A(l,5|3,5).
2. Fehler: Der Punkt B heißt B(2,5|2,5) und eingezeichnet ist B(3,5|2,5).
3. Fehler: Der Punkt E heißt E(0|5) und eingezeichnet ist E(5|0).
4. Fehler: Der Punkt F heißt F(5|4,5) und eingezeichnet ist F(5,5|4,5).
5. Fehler: Der Punkt G heißt G(6|2) und eingezeichnet ist G(6|2,5).
152 – Zeichne in ein geeignetes Quadratgitter:
Eine Gerade g geht durch die Punkte A(l,5|1) und B(4|2).
a) Zeichne eine zu g parallele Gerade k, die den Abstand 1 cm hat.
Wie viele Lösungen gibt es?
b) Zeichne eine senkrechte Gerade p zu g durch den Punkt B.
Lösung:

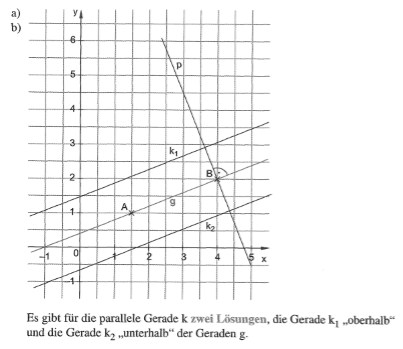
153 – Zeichne ein Quadratgitter (Größe: 6 cm x 6 cm, Seitenlänge der Quadrate: 0,5 cm).
Zeichne alle Gitterpunkte ein, deren Rechtswert größer als 2 und kleiner als 5 ist. Trage in dasselbe Quadratgitter alle Gitterpunkte ein, deren Hochwert kleiner als 4,5 und größer als 1,5 ist.

Lösung:
 

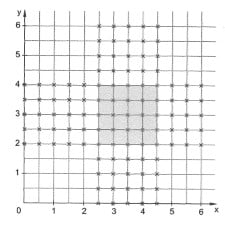
Die roten Punkte sind doppelt besetzt. Diese Punkte erfüllen die Erfordernisse von beiden genannten Bedingungen.