In der Umwelt, in der Natur und im täglichen Leben begegnen dir sehr viele spiegelbildliche Figuren. Sie haben in der Mathematik einen besonderen Namen, man nennt sie achsensymmetrische Figuren. Das Wort Symmetrie kommt aus dem Griechischen und bedeutet in etwa „Ebenmaß“.

Auch in der Geometrie kommen achsensymmetrische Figuren vor. Die Achse, welche die beiden Hälften dieser Figuren trennt, nennt man Symmetrieachse oder Spiegelachse.

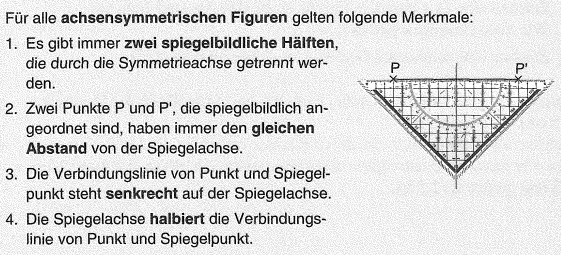
1. Spiegelbildliche Figuren kann man auf verschiedene Arten auch selbst hersteilen:
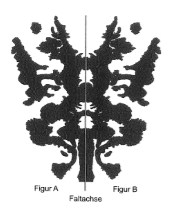
• Kleckse etwas Tinte auf eine Hälfte eines Papiers. Falte das Papier zusammen. Nach dem Auseinanderfalten zeigt sich eine spiegelbildliche Figur mit der Faltachse als Spiegelachse.
• Falte ein Papier und stich mehrere Löcher hinein. Falte es danach auseinander und verbinde die Einstichstellen.

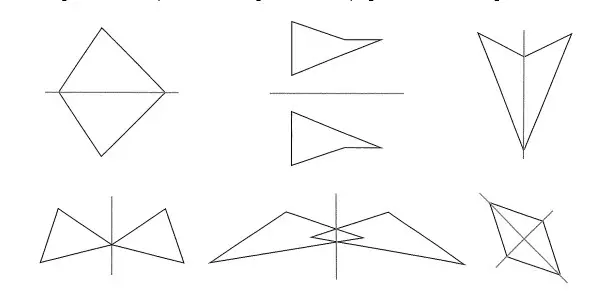
2. Bei folgenden achsensymmetrischen Figuren sind die Spiegelachsen bereits eingezeichnet.

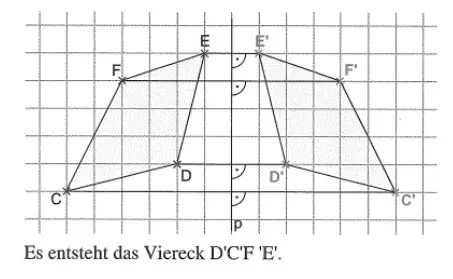
3. Spiegle die Figur CDEF an der Achse p. Welche Figur entsteht?
Lösung:

155 – Wie viele Symmetrieachsen hat folgende Figur?

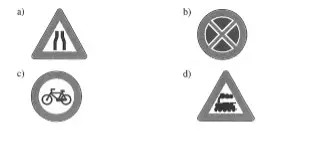
157 – Trage in den Verkehrszeichen die Symmetrieachsen ein, soweit vorhanden.

Lösung :

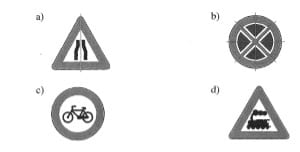
Die Verkehrsschilder c und d haben 0 Symmetrieachsen.

Das Verkehrsschild a hat 1 Symmetrieachse.

Das Verkehrsschild b hat 4 Symmetrieachsen.

158  – Betrachte unten stehendes Alphabet.
a) Nenne alle Buchstaben, die eine Symmetrieachse haben.
b) Welche Buchstaben haben keine Symmetrieachse?
c) Welche Buchstaben haben zwei Symmetrieachsen?
d) Gibt es Buchstaben, die mehr als zwei Symmetrieachsen aufweisen?

Lösung:
a) 1 Symmetrieachse:
A, B, C, D, E, M, T, U, V, W, Y
b) 0 Symmetrieachsen:
F, G, J, K, L, N, P, Q, R, S, Z
c) 2 Symmetrieachsen:
H, I, O, X
d) nein
Es kommt auf die Schriftart an, ob und wie viele Symmetrieachsen ein Buchstabe hat. Das „K“ z. B. hat in der Angabe (K) keine Symmetrieachse. Aber in der Schrift „Impact“ z. B. hat es 1 Symmetrieachse (K). Das „O“ ist nicht kreisförmig, sondern ein wenig höher als breit. Deswegen hat es auch nur 2 Symmetrieachsen. Ein kreisrundes 0 hätte unendlich viele Symmetrieachsen.