Im Alltag begegnen dir Brüche in der Musik (Noten: Halbe, Viertel oder Achtel), in der Küche (eine halbe Pizza, drei Viertel des Kuchens) und im Sport (im zweiten Drittel des Eishockeyspiels, eine Fußball-Halbzeit).
Diese „neuen“ Zahlen heißen Bruchzahlen oder Brüche. Eine Bruchzahl entsteht, wenn ein Ganzes in gleich große Teile geteilt wird. Wird ein Ganzes in 2, 3, 4, … gleich große Teile zerlegt, so entstehen Halbe, Drittel, Viertel, …

Beispiel :

Das Sechseck wird in 6 gleich große Dreiecke unterteilt. Davon werden 5 Dreiecke genommen. Der Bruchteil heißt 5/6
2. Kreise eignen sich gut zur Veranschaulichung von Brüchen
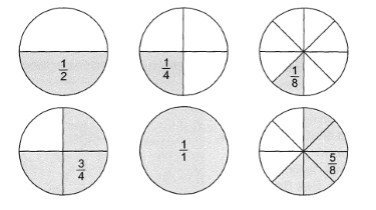
211 – Welcher Bruch ist dargestellt (grau markiert)?
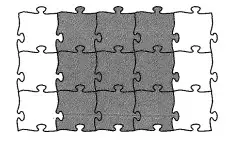
Lösung:
Das Puzzle hat insgesamt 15 Teile. Davon sind 9 eingefärbt. Der Bruchteil beträgt demnach 9 von 15 oder . 9/15.
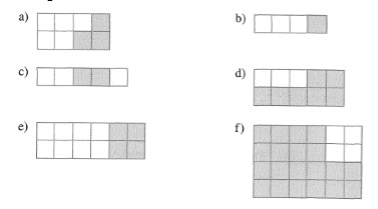
212 – Zeichne jeweils ein geeignetes Rechteck und färbe davon ein:

Lösung:
213 – Gib an, welche Bruchteile der Mauer hellrot, mittelrot und dunkelrot eingefärbt sind.

Lösung:

- Ist der Zahler kleiner als der Nenner, so spricht man von einem echten Bruch.
- Ist der Zahler gröber als der Nenner, so spricht man von einem unechten Bruch.
Man kann ein und denselben Bruch auf verschiedene Weisen darstellen:
• mit Bruchstrich
• mit Divisionszeichen
• mit Worten
Beispiele

214 – Schreibe als Bruch:
a) 1:15 b) 10:11
c) 1:1 d)drei von sieben
e) neun von dreizehn f) zwei von neunzehn
g) vier Fünftel h) drei Siebtel
i) ein Zehntel j) vierzehn Siebzehntel
Lösung :

215 – Wie viel fehlt zu einem Ganzen?

Lösung :
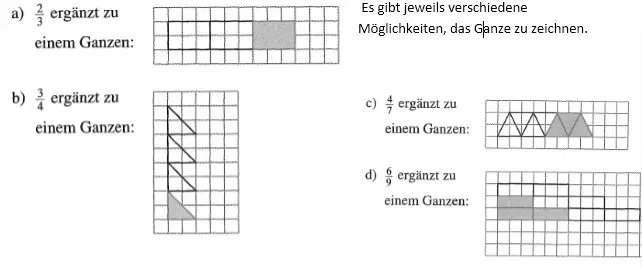
216 – Vervollständige folgende Figuren durch Zeichnung zu einem Ganzen:
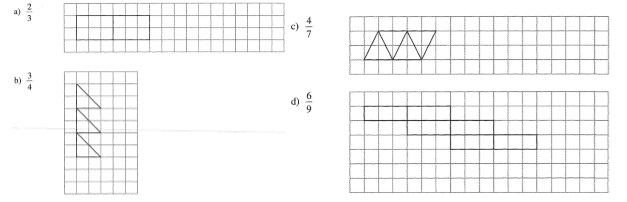
Lösung :
Bruchteile einer Zahl berechnet man, indem man die Zahl durch den Nenner dividiert und anschliebend mit dem Zahler multipliziert.