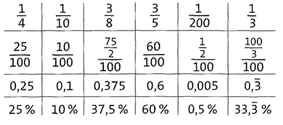
Übung 26 Ergänze die Tabelle.

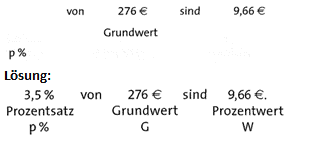
Übung 27 Ergänze die fehlenden Angaben.

Lösung :

WİSSEN

Tipps für schnelles Kopfrechnen
Kennst du wichtige Prozentangaben auswendig, rechnest du sicherer und schneller!

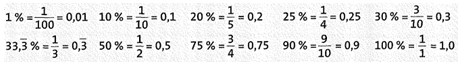
Hast du diese Zahlen immer parat, kannst du viel schneller rechnen:
– 50 % von 4 kg sind die Hälfte, also rechnest du 4 kg : 2 = 2 kg.
– 25 % einer Wegstrecke sind 8 km, 100 % sind demnach 4 • 8 km = 32 km.

Für schnelles Rechnen (mit und ohne Taschenrechner):
– Du willst 15 % von 230 berechnen.
Du weißt: 15 % = 0,15. Also rechnest du W = 0,15 • 230 = 34,5.
– Du willst 7,5 % von 111 bestimmen.
Du weißt: 7,5 % = 0,075. Also rechnest du W = 0,075 • 111 = 8,325.
Auch beim Kopfrechnen gilt: Der einfache Dreisatz (↑ Kap. 4.3) funktioniert immer!

Übung 28 Berechne jeweils den Prozentwert W.
1 % von 750                        10 % von 48                        75 % von 32                        12 % von 84
25 % von 24                       200 % von 200                   0,5 % von 120                    33,3% von 99

Lösung:               
linke Spalte: 7,5; 24; 6; 0,6 rechte Spalte: 4,8; 10,08; 400; 33

Übung 29 Berechne jeweils die Grundmenge G.
a) W = 7; p = 25                b) W = 2,5; p = 10            c) W = 322,45; p = 50
d) W = 125; p = 250         e) W = 600; p = 60           f) W = 222; p = 0,01

Lösung:               
a) 28; b) 25; c) 644,9; d) 50; e) 1000; f) 2 220 000

Übung 30 In den Klassen 6a und 6b ist dieselbe Klassenarbeit geschrieben worden.
In der Klasse 6a wurden 8 von 25 und in der Klasse 6b wurden 9 von 30 Arbeiten mit „gut“ bewertet. Vergleiche die prozentualen Anteile.

Lösung:               
In der 6a haben 32 % der Schüler mit der Note „gut” abgeschnitten, in der 6b nur 30 %. Also hat in der 6a ein größerer Anteil der Schüler mit „gut“ abgeschnitten.

Übung 31 Ein schöner Stuhl kostete bisher 84 €, jetzt wurde der Preis aber um 10 % erhöht. Ein Stammkunde erhält auf diesen erhöhten Preis 10 % Rabatt. Wie viel muss er zahlen?

Lösung:               
Er muss 83,16 € bezahlen.

Übung 32 Zum Nettopreis einer Handwerkerrechnung kommen 16 % Mehrwertsteuer hinzu. Wie viel Euro beträgt die Mehrwertsteuer, wenn der Nettopreis 270 € beträgt?

Lösung:               
Die Mehrwertsteuer beträgt 43,20 €.

WİSSEN

Kreisdiagramme

Kreisdiagramme
Anteile werden häufig in Kreisdiagrammen veranschaulicht.
Der Vollkreis (360°) entspricht dem Grundwert G.
Für jeden der Prozentsätze wird ein Kreissegment gekennzeichnet,
das den entsprechenden prozentualen Anteil am Vollkreis hat.

Um selbst ein Kreisdiagramm zu zeichnen, musst du für jeden Anteil
berechnen, welcher Mittelpunktswinkel ihm entspricht.

Beispiel: Ein Anteil von 25 % wird so dargestellt:
100% -> 360°
1 % -> 3,6°
25% ->  90°

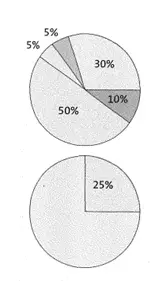
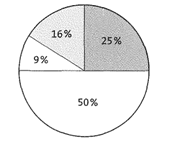
Übung 33 Bearbeite das untere der beiden abgebildeten Kreisdiagramme.
a) Markiere Kreissegmente, die 50 % bzw. 9 % darstellen.
b) Welchen Prozentsatz macht der letzte verbleibende Anteil am Ganzen aus?

Lösung:

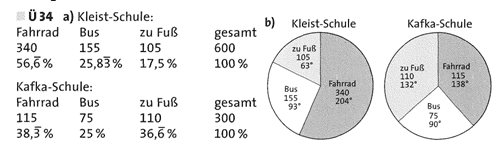
Übung 34 An der Heinrich-von-Kleist-Schule werden 600 Schüler unterrichtet. Davon kommen 340 mit dem Fahrrad, 155 mit dem Bus und 105 zu Fuß zur Schule. Von 300 Schülern der Franz-Kafka-Schule kommen 115 mit dem Fahrrad, 75 mit dem Bus und 110 zu Fuß.

a) Erstelle eine Tabelle im Heft und vergleiche die prozentualen Anteile.
b) Erstelle für jede Schule ein Kreisdiagramm. Färbe entsprechende Anteile jeweils gleich.

Lösung:

WİSSEN
Zinsrechnung
Wenn du Geld auf einem Konto sparst, bekommst du dafür Zinsen. Das bedeutet, dass du einen bestimmten prozentualen Anteil dazu bekommst. Diese Zinsen werden mithilfe der Prozentrechnung berechnet. Es werden lediglich andere Bezeichnungen verwendet.

Lisa hat 250 € auf ihrem Sparbuch angelegt, diese werden mit einem jährlichen Zinssatz von 2 % verzinst. Wie viel Zinsen bekommt Lisa am Jahresende zu ihrem Kapital hinzu?
Gegeben: K = 250 €, p % = 2 %, gesucht: Z

Herr Schröder musste sich Geld zu einem Zinssatz von 9 % leihen. Nach einem Jahr sind 360 € Zinsen zu bezahlen. Wie viel Geld hat er sich geliehen?
Gegeben: p % = 9 %, Z = 360 €, gesucht: K.

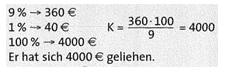
Üblicherweise bezieht sich der Zinssatz auf ein Jahr, man spricht auch vom Jahreszinssatz. Natürlich kann man auch berechnen, wie viel Zinsen man dann an einem Tag, an x Tagen oder auch in x Wochen oder Monaten bekommt. Die Banken haben sich darauf geeinigt, grundsätzlich von 360 Tagen im Jahr auszugehen.

Übung 35 Welchen Jahreszins bekommt man für 225 € bei einem Zinssatz von 6 %?
Lösung:
Man bekommt 13,50 €.

Übung 36 Udo kauft für 15 000 € Aktien, die er ein Jahr später für 16 650 € verkauft.
a) Wie viel Prozent Gewinn hat er gemacht?
b) Wie viel Zinsen hätte er bekommen, wenn er das Angebot der Bank angenommen hätte, die ihm einen Zinssatz von 8 % angeboten hatte?
c) Herr Bär hat bei seiner Bank Geld zu einem Zinssatz von 9,5 % angelegt. Am Jahresende werden ihm 1900 € überwiesen. Wie viel Geld hat er angelegt?

Lösung:
Ü 36 a) Er hat 11 % Gewinn erzielt.
b) Er hätte 1200 € Zinsen bekommen.
c) Er hat 20 000 € angelegt.

Übung 37 Herr Schmidt hat eine Million Euro so angelegt, dass sie mit 12 % verzinst werden. Wie viel Zinsen bekommt er an einem Tag, in einer Woche bzw. in einem Vierteljahr? Wie lange dauert es, bis er 33 000 € Zinsen bekommen hat?

Lösung:
Er bekommt 333,33 € pro Tag. In einer Woche bekommt er 2333,33 €; in einem Vierteljahr 30 000 €.
Es dauert 99 Tage.