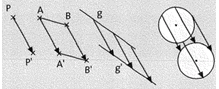
Eine Verschiebung ist eine Abbildung, die durch einen Verschiebungspfeil v eindeutig festgelegt wird. Der Pfeil bestimmt die Länge (den Betrag) und die Richtung der Verschiebung.

Jedem Originalpunkt P wird eindeutig ein Bildpunkt P’ zugeordnet. Die Pfeile von P nach P’, A nach A’ usw. sind parallel zueinander.
Das Original und sein Bild sind kongruent (deckungsgleich).
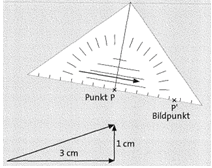
Verschiebung eines Punktes P:
1. Miss die Länge des Verschiebungspfeils.
2. Lege das Geodreieck mit der Null an P, sodass die Linealkante (Grundseite) parallel zum Verschiebungspfeil liegt.
3. Trage die Länge des Verschiebungspfeils ab und markiere den Bildpunkt P’
Die Angabe eines Verschiebungspfeils kann auch in Worten erfolgen: „Verschiebe das Viereck um 3 cm nach rechts und um 1 cm nach oben.“
Es genügt meist, wichtige Punkte einer Figur (z. B. Eckpunkte) zu verschieben.
Es gilt nämlich:
Das Bild einer Strecke ist eine gleich lange parallele Strecke.
Das Bild eines Winkels ist ein gleich großer Winkel.
Das Bild einer Geraden ist eine zu ihr parallele Gerade.
Das Bild eines Kreises ist ein Kreis mit demselben Radius.
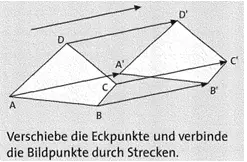
Übung 1 Verschiebe die Figuren so, wie es der Verschiebungspfeil angibt. Zeichne in dein Übungsheft.
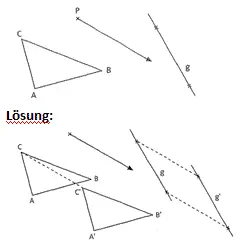
Übung 2 Beschreibe die Verschiebung aus Übung 1: Gib ihre Länge in cm an und ihre Richtung als Uhrzeit (Beispiel: „senkrecht nach unten“ ist 6 Uhr).
Lösung:
Richtung: 4 Uhr; Länge: 2,5 cm
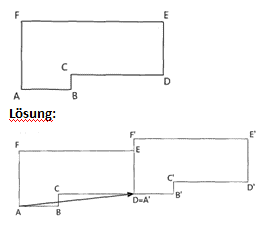
Übung 3 Es gibt eine Verschiebung, die A auf D abbildet. Zeichne dafür einen Pfeil und verschiebe damit die gesamte Figur. Zeichne in dein Übungsheft.
WİSSEN
Verschiebungssymmetrie
Eine Figur heißt verschiebungssymmetrisch, wenn sie durch eine Verschiebung auf sich selbst abgebildet werden kann. Eine solche Figur heißt auch Ornament.
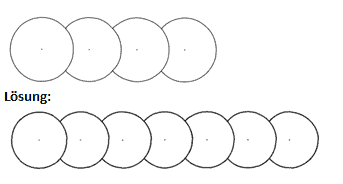
Übung 4 In dem Muster kann man mehrere Verschiebungssymmetrien entdecken. Setze es entsprechend fort.

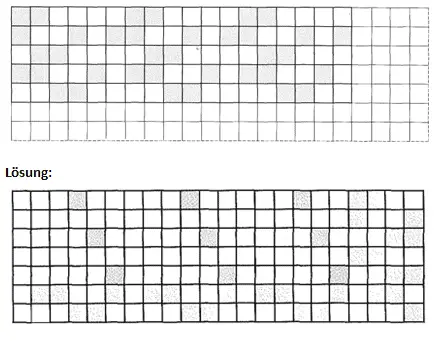
Übung 5 Einen Kreis verschiebt man, indem man seinen Mittelpunkt verschiebt und den Radius beibehält. Miss das Muster aus, übertrage es in dein Übungsheft und setze es nach rechts fort.