Eine Punktspiegelung ist eine Drehung (t Kap. 6.2) um 180°.
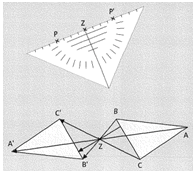
Punktspiegelung eines Punktes P:
1. Lege das Geo-Dreieck mit der Null so an das Spiegelzentrum Z, dass die Linealkante (Grundseite) durch P geht.
2. Übertrage die Entfernung von P zu Z auf die andere Seite der Linealkante. Markiere den Bildpunkt P’.
Es genügt, wichtige Punkte zu spiegeln, denn Strecken und Winkel bleiben bei der Punktspiegelung gleich groß; Geraden werden auf Geraden und Kreise werden auf Kreise mit gleichem Radius abgebildet.

Achsenspiegelung
Eine Achsenspiegelung ist eine Abbildung, die durch Angabe einer Spiegelachse g eindeutig festgelegt ist. Die Punkte einer Figur werden entlang der Spiegelachse auf deren andere Seite gespiegelt. Original und Bild sind kongruent (deckungsgleich). Jedem Originalpunkt P wird eindeutig ein Bildpunkt P’ zugeordnet. Alle Punkte von g werden auf sich selbst abgebildet.

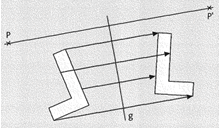
Achsenspiegelung eines Punktes P:
1. Lege die Mittellinie des Geodreiecks so auf g, dass seine Linealkante (Grundseite) durch P geht.
2. Übertrage die Entfernung von P zu g auf die andere Seite der Linealkante.
Es genügt, wichtige Punkte zu spiegeln, denn Strecken und Winkel bleiben bei der Achsenspiegelung gleich groß; Geraden werden auf Geraden und Kreise werden auf Kreise mit gleichem Radius abgebildet.

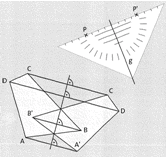
Übung 12 Zeichne die folgenden Punkte A (5|0), B (4|2), C (5|5), O (3|0), R (4|6) und Z (6(3) in ein Koordinatensystem. Zeichne das Dreieck ABC und die Gerade g durch O und R ein.

a) Konstruiere das Dreieck A’ B’ C durch Spiegelung von ABC an der Achse g.
b) Konstruiere das Dreieck A” B” C” durch Spiegelung von ABC am Punkt Z.

Lösung:
A’ (1,1|0,6); B’ (2,7|2,2); C’ (2,7|5,4) A” (716); B” (8|4); C” (7|1)

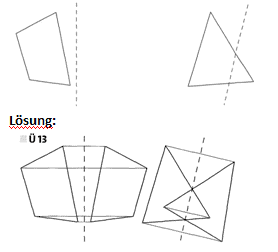
Übung 13 Führe mithilfe des Geodreiecks je eine Achsenspiegelung aus.
(Tipp: Eine Spiegelachse kann auch innerhalb einer Figur liegen. Die Bilder der (Eck-)Punkte liegen dabei immer auf der jeweils anderen Seite der Achse.)

Übung 14 Spiegle jede der Figuren am eingezeichneten Spiegelzentrum Z.

 

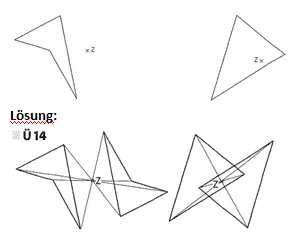
Übung 15 Spiegle jede der Figuren mithilfe der Kästchen an der eingezeichneten Spiegelachse.

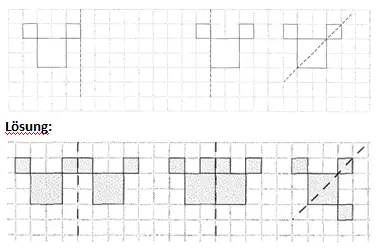
WİSSEN

Punkt – und achsensymmetrische Figuren
Lässt sich eine Figur durch eine Punktspiegelung auf sich selbst abbilden, so heißt sie punktsymmetrisch.
Drehe zur Probe das Buch um 180°. Die oberen vier Figuren ändern ihr Ausseher nicht.
Figuren, die durch eine Achsenspiegelung auf sich selbst abgebildet werden können, nennt man achsensymmetrisch Achsensymmetrische Figuren können auch mehrere Symmetrieachsen haben.

Übung 16 Zeichne zu jeder der Figuren alle Symmetrieachsen ein.
(Tipp: Drehe das Buch und betrachte die Figuren aus unterschiedlichen Blickwinkeln.)

Übung 17 Gib zu jeder Figur an, ob sie punkt- oder achsensymmetrisch (oder beides) ist. Nenne außerdem zu jeder achsensymmetrischen Figur die Anzahl der Symmetrieachsen.

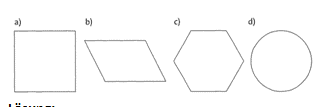
Lösung:
a) punkt- und achsensymmetrisch (4 Achsen)
b) nur punktsymmetrisch
c) punkt- und achsensymmetrisch (6 Achsen)
d) punkt – und achsensymmetrisch (unendlich viele Achsen sind denkbar)

Übung 18 Überprüfe den unten stehenden Satz an einem Beispiel.
Führe dazu an einem Dreieck nacheinander zwei Achsenspiegelungen durch und kontrolliere mithilfe einer Punktspiegelung. Satz: Spiegelt man eine Figur an einer Spiegelachse und dann ihr Bild nochmals an einer zweiten Achse, die orthogonal (rechtwinklig) zur ersten Spiegelachse steht, so entspricht die Abbildung insgesamt einer Punktspiegelung. Das Zentrum dieser Punktspiegelung ist der Schnittpunkt der beiden Spiegelachsen.
Lösung:
Dieser Satz gilt allgemein!