Der Flächeninhalt einer Figur ist die Größe der von der Figur umschlossenen Fläche.
Ein Quadrat mit der Seitenlänge 1 cm hat den Flächeninhalt 1 cm2.
Ein Quadrat mit der Seitenlänge 1 cm (m, dm, mm usw.) nennt man Einheitsquadrat.
Um den Flächeninhalt einer Figur zu bestimmen, berechnet man, wie viele Einheitsquadrate in die Figur hineinpassen.
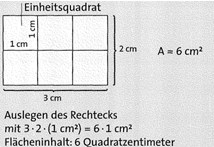
Je nach Größe der zu messenden Fläche, geht man von unterschiedlichen Einheitsquadraten aus.
Um einen Flächeninhalt von mehreren Quadratkilometern zu berechnen, dient z. B. der Quadratkilometer als Einheit.
Ist die Fläche nur einige Quadratzentimeter groß, verwendet man lieber diese Einheit.

Der Flächeninhalt eines Rechtecks mit
den Seitenlängen a und b ist das Produkt der Seiteniängen:
A = a – b
Der Flächeninhalt eines Quadrats mit der
Seitenlänge a ist entsprechend:
A = a • a = a2
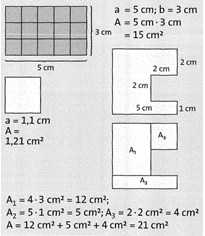
Zerlegung von Flächen:
Lässt sich eine Figur in mehrere Rechtecke zerlegen, so berechnet man die Flächeninhalte der einzelnen Rechtecke und addiert diese.
Übung 1 Zeichne je ein Einheitsquadrat von 1 dm2,1 cm2 und 1 mm2 (arbeite genau!) auf ein Blatt Papier und schneide die Quadrate aus. Schätze mithilfe dieser Quadrate die Größe eines DIN-A4-Blatts und einer EC-Karte.
Lösung:
EC-Karte: ca. 40 cm2, DIN-A4-Blatt: ca. 6 dm2
Übung 2 Berechne den Flächeninhalt der abgebildeten Rechtecke. Gib beim Ergebnis die Einheit mit an. (Die Rechtecke sind nicht maßstabgetreu gezeichnet, ausmessen hilft hier nicht!)
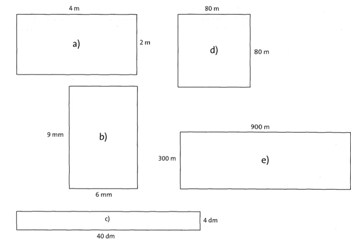
Lösung:
a) 8 m2; b) 54 mm2; c) 160 dm2; d) 6400 m2 = 64 a; e) 270 000 m2 = 27 ha
Übung 3 Bestimme den Inhalt der beiden Flächen. Du kannst zum Messen Geodreieck oder das l-cm2-Einheitsquadrat aus Übung 1 benutzen.
(Tipp: Bei der rechten Figur musst du auch mit halben Einheiten arbeiten.)
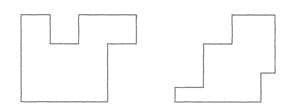
Lösung:
links: 9 cm2; rechts: 6,5 cm2
WİSSEN
Umrechnen von Flächeneinheiten
Bei der Umrechnung von einer Flächeneinheit in die nächstkleinere Einheit wird die Maßzahl mit 100 multipliziert.
Bei der Umrechnung von einer Flächeneinheit in die nächstgrößere Einheit wird die Maßzahl durch 100 dividiert.

Multiplikation mit 100
entspricht dem Anhängen von zwei Nullen;
bzw. verschiebt das Komma in Dezimalzahlen um zwei Stellen nach rechts.
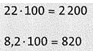
Division durch 100
– entspricht dem Streichen von zwei Nullen;
– bzw. verschiebt das Komma in Dezimalzahlen um zwei Stellen nach links.
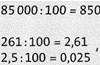
Übung 4 Berechne die Flächeninhalte der einzelnen Rechtecke. Gib das Ergebnis immer in der Einheit an, in der die Maßzahl möglichst wenig Nullen hat.
Beispiel: a = 40 m; b = 50 m; Flächeninhalt A = 40 m • 50 m = 2 000 m2 = 20 a
- a) a = 3dm; b = 4dm b) a = 10cm; b = 20cm
- c) a = 7 mm; b = 5 mm d) a = 6 km; b = 50 km
- e) a = 150 m; b = 10 m f) a = 200 m; b = 200 m
- g) a = 12 mm; b = 50 mm h) a = 2 000 m; b = 500 m
Lösung:
a) 12 dm2; b) 2 dm2; c) 35 mm2; d) 300 km2; e) 15 a; f) 4 ha; g) 6 cm2; h) 1 km2
Übüng 5 Schreibe in dein Übungsheft den Flächeninhalt in der nächstkleineren Einheit.
Beispiele: 22 km2 = 2 200 ha; 120 m2 = 12 000 dm2
- a) 5 km2 b) 11dm2 c) 12 a d) 107 m2
- e) 20 cm2 f) 200 ha g) 202 cm2 h) 100 m2
Lösung:
a) 500 ha; b) 1100 cm2; c) 1200 m2; d) 10 700 dm2; e) 2000 mm2; f) 20 000 a; g) 20 200 mm2;
h) 10 000 dm2
Übung 6 Schreibe in dein Übungsheft den Flächeninhalt in der nächstgrößeren Einheit. Beispiele: 200 ha = 2 km2; 80 000 m2 = 800 a
- a) 500 ha b) 1500 cm2 c) 25 000 m2 d) 2 000 mm2
- e) 100 a f) 202 000 cm2 g) 4 500dm2 h) 22 200 a
Lösung:
a) 5 km2; b) 15 dm2; c) 250 a; d) 20 cm2; e) 1 ha; f) 2020 dm2; g) 45 m2; h) 222 ha
Übung 7 Rechne Länge oder Breite so um, dass jeweils beide Angaben dieselbe Einheit tragen. Berechne anschließend den Flächeninhalt.
Beispiel: a = 7 dm; b = 5 cm; Flächeninhalt A = 7 dm • 5 cm = 70 cm • 5 cm = 350 cm2
- a) a = 3dm; b = 4cm b) a = 12 m; b = 2 dm
- c) a = 70mm; b = 3cm d) a = 2dm; b = 80cm
- e) a = 50mm; b = 8dm f) a = 6km; b = 3000m
- g) a = 200 m; b = 5 km h) a = 15 cm; b = 2 m
Lösung:
a) 120 cm2; b) 240 dm2; c) 2100 mm2 21 cm2 d) 1600 cm2 = 16 dm2; e) 40 000 mm 4 dm2
f) 18 000 000 m2 = 18 km2; g)1000 000 m2 = 1km2; h) 3000 cm2 = 30 dm2
Übung 8 Peter will sein Zimmer neu streichen. Hilf beim Rechnen!
„Mein Zimmer ist drei Meter breit und vier Meter lang. Ich brauche Farbe für die Decke und für die Wände. Die Wände sind drei Meter hoch.
Im Eimer ist Farbe für 50 m2. Meinst du, das reicht?”
Lösung:
Die Gesamtfläche (4 Wände und 1 Decke) beträgt 54m2. Die Farbe reicht nicht.
Übung 9 Schreibe in dein Übungsheft den Flächeninhalt jeweils in der nächstgrößeren Einheit. Achte auf das Komma!
Beispiele: 20 ha = 0,2 km2; 8,1 mm2 = 0,081 cm2
- a) 50ha b) 160cm2 c) 50 m2 d) 4mm2
- e) la f) 17,4cm2 g) 110,5 ha h) 0,2 dm2
Lösung:
a) 0,5 km2; b) 1,6 dm2; c) 0,5 a; d) 0,04 cm2; e) 0,01 ha; f) 0,174 dm2; g) 1,105 km2; h) 0,002 m2
Übung 10 Schreibe die Größe jeweils in der angegebenen Einheit.
Beispiel: 45 dm2 (in mm2); Rechnung 45 dm2 = 4 500 cm2 = 450 000 mm2
- a) 4 km2 (in a) b) 150 m2 (in cm2) c) 2 m2 (in mm2)
- d) 500 000 m2 (ha) e) 7 000 000 m2 (in cm2) f) 10 000 000 cm2 (in a)
- g) 4,22 m2 (in cm2) h) 0,005 m2 (in cm2) i) 120 cm2 (in m2)
Lösung:
a) 40 000 a; b) 1 500 000 cm2; c) 2 000 000 mm2; d) 50 ha; e) 70 000 000 000 cm2; f) 10 a;
g) 42 200 cm2 h) 50 cm2; i) 0,012 m2
Übung 11 Der Umfang eines Rechtecks ist die Summe der vier Seitenlängen. Da je zwei Seiten gleich lang sind, schreibt man kurz u = 2 • a + 2 • b.
Ergänze in der Tabelle die fehlenden Werte.
