Das Volumen V (der Rauminhalt) eines Körpers ist die Größe des vom Körper ausgefüllten Raumes.

Ein Würfel mit der Kantenlänge 1 cm hat das Volumen 1 cm³.

Einen Würfel mit der Kantenlänge 1cm (m, dm, mm usw.) nennt man Einheits­würfel.

Zur Bestimmung seines Volumens kann man einen Körper mit Einheitswürfeln füllen.

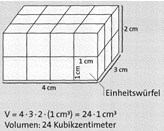
Je nach Größe des zu messenden Rauminhalts geht man von unterschiedlichen Einheitswürfeln aus.
Um ein Volumen von mehreren Kubikzentimetern zu berechnen, dient beispielsweise der Kubikzentimeter als Einheit.

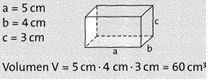
Fasst man Länge mal Breite als Inhalt der Grundfläche (also G = a • b) auf und bezeichnet man die Höhe mit h, so kann man das Ouadervolumen auch so berechnen: V = G • h

Bei der Umrechnung von einer Einheit zur nächstkleineren, wird die Maßzahl mit 1000 multipliziert.

Bei der Umrechnung von einer Einheit in die nächstgrößere Einheit, wird die Maßzahl durch 1000 dividiert.

Im Alltag verwendet man auch Liter (1l ) und Milliliter (1ml) als Einheiten:

1I = 1 dm³ = 1000ml; 1 ml = 1 cm³

Übung 34 Baue ein Modell eines Einheitswürfels von 1dm³.

Stelle dir vor, wie groß 1 cm³ und 1 m³ sind.

Schätze, wie groß in etwa die Volumina folgender Körper sind: dieses Buch, ein Stecknadelkopf, eine
Tintenpatrone, eine Badewanne, dein Zimmer.

Lösung:
Buch: 400 cm³; Stecknadel köpf: 3 mm³; Tintenpatrone: 1 cm³; Badewanne: 400 dm³; Zimmer: 30 m³

Übung 35 Erkläre, warum genau 1000 Einheitsquader von 1 cm³ in 1 dm³ passen.
Lösung:
Der große Würfel wird systematisch mit den kleinen gefüllt. Je 10 kleine passen dabei in eine Reihe. 10 Reihen passen auf die Grundfläche. 10 solcher Schichten übereinander füllen den ganzen Würfel: 10 • 10 • 10 = 1000.

Übung 36 Berechne aus den Kantenlängen der Quader jeweils das Volumen.

Beispiel: a = 100 cm; b = 12 cm; c = 20 cm

Rechnung: V = 100 cm • 12 cm • 20 cm = 24 000 cm³ = 24 dm³

a) a = 2 m; b = 3 m; c = 5 m b) a = 15 cm; b = 3 cm; c = 5 cm
c) a = 10cm; b = 200cm; c = 20cm d) a = 1dm; b = 40dm; c = 750dm
e) a = 200 mm; b = 250 mm; c = 1000 mm

Lösung:
a) 30 m³; b) 225 cm³; c) 40 000 cm³ = 40 dm³; d) 30 000 dm³ = 30 m³; e) 50 000 000 mm³ = 50 dm³

Übung 37 In einer Straße wird eine Gasleitung verlegt. Dazu wird ein Graben ausgehoben, der 50 m lang, 1 m breit und 2 m tief ist.

a) Wie viele Kubikmeter Erde müssen ausgehoben werden?
b) Wie viele Tonnen sind das, wenn 1 m³ Erde ca. 3 Tonnen wiegt?

Lösung:
a) Es müssen 100 m³ Erde ausgehoben werden; b) 100 m³ Erde wiegen300t.

Übung 38 Ergänze die Lücken in der Tabelle.

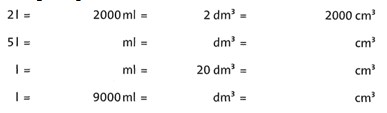
Lösung:
2l = 2 000 ml = 2dm³ = 2 000 cm³
5l= 5 000 ml =    5dm³=  5 000 cm³
20l = 20 000 ml  = 20 dm³ = 20 000 cm³
9 l = 9 000 ml =  9dm³=  9 000 cm³

WİSSEN

Multiplikation mit 1000 und Division durch 1000

Multiplikation mit 1000 (T Kap. 2.2) entspricht dem Anhängen von drei Nullen bzw.
verschiebt das Komma in Dezimalzahlen um drei Stellen nach rechts. Division durch 1000 (T Kap. 2.2) entspricht dem Streichen von drei Nullen bzw. verschiebt das Komma in Dezimalzahlen um drei Stellen nach links.

Übung 39 Schreibe in dein Übungsheft jeweils in der nächstkleineren Einheit.

Beispiele: 15 m³ = 15 000 dm³; 2,05 cm³ = 2 050 mm3

a)5m³                    b)8dm³                 c)20cm³               d) 500 cm³          e) 1010 m³          f) 2 000 cm³
g) 0,5 dm³           h) 3,2 m³             i) 70,05 m³          j) 41                       k)0,5 I                   l)0,025  1

Lösung:
a) 5000 dm³;                      b) 8000 cm³;       c) 20 000 mm³;      d) 500 000 mm³;           e) 1010 000 dm³;
f) 2 000 000 mm³;            g) 500 cm³;         h) 3200 dm³;          i) 70 050 dm³;               j) 4000 ml;
k) 500 ml; I) 25 ml

Übung 40 Schreibe in dein Übungsheft jeweils in der nächstgrößeren Einheit. Beispiele: 4 000 mm³ = 4 cm³; 12 dm³ = 0,012 m³

Lösung:
a) 8 cm³; b) 58 cm³; c) 25 dm³;    d) 125 m³;    e) 1000 dm³;    f) 3,3 m³;    g) 0,5 dm³;    h) 0,05 cm³; İ) 0,002 m³;    j) 4 I;    k) 1,5 I; I) 0,025 I
Übung 41 Rechne jeweils zuerst in dieselbe Maßeinheit um. Berechne anschließend das Volumen des Quaders.

Beispiel: a = 4 cm, b = 5 dm, c = 25 cm

V = 4 cm • 5 dm • 25 cm = 4 cm • 50 cm • 25 cm = 5000 cm³ = 5 dm³

a) a = 2cm; b = 10cm; c = 3dm
b)a = 70dm;b = lm;c = 3m
c) a = 800 mm; b = 25 cm; c = 3 dm
d) a = 0,2 dm; b = 35 cm; c = 0,5 dm

Lösung:
a) 600 cm³; b) 21 m³; c) 60 dm³; d) 350 cm³

Übung 42 Eine Packung H-Milch hat die folgenden Abmessungen:
Länge: 9,2 cm; Breite 5,5 cm; Höhe: 19,5 cm. Berechne ihr Volumen und gib das Ergebnis der Einheit Liter an. In der Packung soll ein Liter Milch sein. Erkläre die Abweichung.

Lösung:
V = 986,7 cm³ = 0,9867 Liter. Milchpackungen sind nicht exakt quader­förmig, sondern etwas bauchig.

Übung 43 Bestimme die Volumina der Körper (Maße in cm).

Anleitung: Zerlege jeden Körper in Ouader und bestimme die Volumina der einzelnen Teilquader. Anschließend addierst du jeweils die Volumina aller Teilquader und erhältst so das Gesamtvolumen des Körpers.

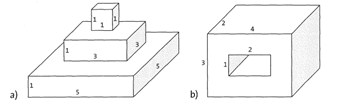
Lösung:
a) 35 cm³; b) 20 cm³ (Kann auch durch Subtraktion gelöst werden.)

Übung 44 Ein Tropfen Öl hat das Volumen 50 mm3. Gibt man ihn auf eine Wasseroberfläche, so entsteht ein Fleck, der ungefähr 5 cm lang und 5 cm breit ist. Bereche die Höhe dieses Ölflecks.

Lösung: