In diesem Lerntrainer kommen Begriffe vor, die dir bekannt sein müssen, damit du erfolgreich arbeiten kannst. Mit Übung 1 prüfst du dein Vorwissen.

Übüng 1
Notiere die Bedeutung der folgenden Begriffe mit eigenen Worten.

Natürliche Zahl, Bruchzahl, Kehrwert (Kehrbruch), Hauptnenner, Quotient, Produkt, Zahlenstrahl, «Punkt-vor-Strich »-Rechnung

Überprüfe die Übung mit Hilfe des Lösungsteils.
Wenn du bei mehreren Begriffen unsicher warst, lies im klipp klar Lerntrainer «Dezimalbruchrechnung»
(Nr. 60394) nach.
Du lernst jetzt einige Bezeichnungen kennen, die häufig Vorkommen und mit denen du mathematische Sachverhalte darstellst.

Lösung:
Natürliche Zahl: eine der Zahlen 0; 1; 2; 3 usw.
Bruchzahl: Bruch wie ½ oder 2/3
Kehrwert (Kehrbruch): Werden bei einem Bruch Zähler und Nenner vertauscht, dann entsteht der Kehrwert (Kehrbruch).
Hauptnenner: kleinster gemeinsamer Nenner von Brüchen Quotient: a:b ist der Quotient aus den Zahlen a und b (Ergebnis einer Division). Produkt: ab ist das Produkt aus den Zahlen a und b (Ergebnis einer Multiplikation). Zahlenstrahl: dient zur graphischen Darstellung von Zahlen.
«Punkt-vor-Strich»-Rechnung: Punkt-Rechnung geht vor Strich-Rechnung. Deshalb geht Multiplikation vor Addition.
Tipp: Kopiere und vergrößere diese Begriffsbestimmungen und lerne sie auswendig.

Biespiel

Beachte, dass alle natürlichen Zahlen zu den Bruchzahlen gehören. Jede natürliche Zahl lässt sich nämlich als Bruch schreiben.

Biespiel

sind Bruchzahlen. Du erkennst durch Kürzen, dass diese Bruchzahlen nur eine andere Schreibweise für die natürliche Zahl 4 sind.

Übung 2
Lies und erläutere die folgenden Zeichenreihen. Schreibe in deinem Heft jeweils ein Beispiel dazu.

Überprüfe nun deine Lösungen.
Auch die natürliche Zahl 0 gehört zu IB. Jede Bruchzahl mit dem Zähler 0 und einem beliebigen Nenner ungleich 0 ist nur eine andere Schreibweise für die Zahl 0.

Lösung:
a) a ist Element von IN. Beispiel: a = 2.
b) y ist Element von IN. Beispiel: y = 3.
c) y ist Element von IB. Beispiel: y = ½

Bearbeite Aufgaben, bei denen du zu falschen Lösungen gekommen bist, noch einmal.

Biespiel
sind andere Schreibweisen für die Zahl 0.

Übung 3
Welche der folgenden Aussagen sind wahr (notiere w), welche sind falsch (notiere f)?

Lösung:
a) w b) w c) w, denn 3 kann auch als Bruch (  )geschrieben werden d) f e) f

Übung 4
Schreibe als Brüche.
13; 36; 5; 101

Lösung:
Mögliche Beispiele sind:

Nun geht es um Dezimalzahlen.
Die Zahl 2,5 aus Übung 3 ist eine Dezimalzahl. Solche Zahlen kennst du bereits aus Anwendungsaufgaben, zum Beispiel aus der Prozentrechnung.
Die Ganzen werden durch die natürliche Zahl vor dem Komma angegeben. An der ersten Stelle nach dem Komma stehen die Zehntel, an der zweiten Stelle die Hundertstel, an der dritten die Tausendstel usw.

Biespiel

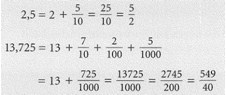
Tipp: Kürzen nicht vergessen.
Auf diese Weise lässt sich jede Dezimalzahl, die endlich viele Stellen nach dem Komma hat, in einen Bruch umwandeln.

Übung 5
Wandle wie im Beispiel in einen Bruch um. Kürze, wenn es möglich ist.
a) 2,72                  b) 0,01                  c) 12,222              d) 101,101

Lösung: