Die Spiegelzahlen auf Seite 24 geben einen Hinweis, wie negative Zahlen dargestellt werden können. Du erweiterst den Zahlenstrahl zu einer Zahlenachse wie in der Abbildung. Rechts von 0 trägst du in gleichen Abständen die natürlichen Zahlen 1,2,3,… ab und links, gespiegelt an 0, die negativen Zahlen -1, -2, -3,… Die Zahlen zwischen den natürlichen Zahlen und den Spiegelzahlen stellst du wie auf Seite 19 dar. Weil es unendlich viele natürliche Zahlen gibt, musst du dir den abgebildeten Ausschnitt nach rechts und links beliebig verlängert vorstellen.
Übung 20
Zeichne eine Zahlenachse. Stelle die Zahlen 3, 1 1/5 , -0,5, -4, -2,86 auf dieser Zahlenachse dar.
Wähle den Ausschnitt geschickt. Wandle 1 1/5 in einen.
Dezimalbruch um.
Verwende gegebenenfalls Näherungen.
Lösung:

(-2,86) wird auf (-2,9) gerundet.
Vorzeichen und Rechenzeichen
Das Vorgesetzte Minuszeichen als Markicrungszcichen für negative Zahlen ist ein Vorzeichen. Es darf nicht mit dem Subtraktionszeichen verwechselt werden. Das Subtraktionszeichen ist ein Rechenzeichen.
Wir setzen eine Klammer um negative Zahlen, damit es nicht zu Verwechslungen kommt.
Biespiel

Diese Schreibweise führt nun dazu, auch bei den positiven Zahlen ein Vorzeichen und eine Klammer zu setzen.
Biespiel

Das Setzen der Klammern ist vor allem bei den positiven Zahlen sehr umständlich. Es hilft dir aber dabei, Vorzeichen und Rechenzeichen streng zu unterscheiden. Du wirst später sehen, dass die Klammern wieder weggelassen werden können, wenn Verwechslungen ausgeschlossen sind.
Hinweis
Terme heißen mathematische Ausdrücke mit Zahlen, Variablen, Rechenzeichen und Rechenklammern. Solche Terme müssen nun umständlicher geschrieben werden, zum Beispiel:

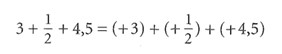
Übung 21
Schreibe mit Vorzeichen.

Lösung:

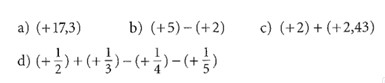
Du weißt jetzt, wie die neuen Zahlen geschrieben werden und wie du sie auf einer Zahlenachse darstellen kannst. Auf der Zahlenachse findest du für jede Zahl auch einen Platz. In der Abbildung sind Beispiele und eine neue Bezeichnung für die Zahlen angegeben.