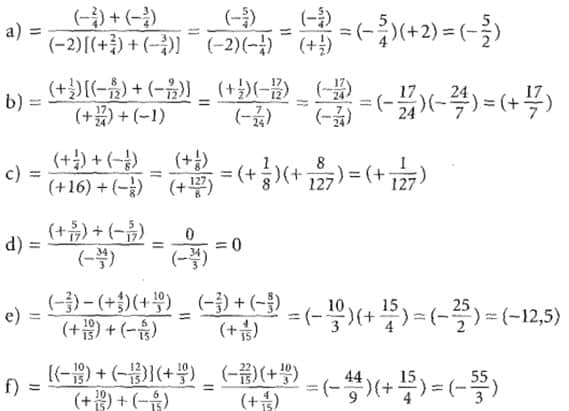Die Subtraktion hast du mit Hilfe der Gegenzahlen auf die Addition rationaler Zahlen zurückgeführt (vergleiche Seite 42). Entsprechend führen wir die Division rationaler Zahlen auf die Multiplikation zurück. Schon beim Rechnen in der Menge IB der Bruchzahlen hast du gelernt, dass die Division durch einen Bruch über die Multiplikation mit dessen Kehrwert (Kehrbruch) erreicht wird.
Der Kehrwert (Kehrbruch) entsteht, wenn Zähler und Nenner vertauscht werden.
Beispiel:

Wenn du diese Kehrwertbildung auf eine beliebige rationale Zahl x überträgst, die nicht Null ist, dann erhältst du:
Übung:
Bestimme den Kehrwert. Wan die (-1,8) in einen Bruch um.
a) (-3)
b) (-1)
c) (+1)
d) (-1,8)
e) (- 1/81 )
Lösung:
a) – 1/3
b) (-1)
c) (+1)
d) -5/9
e) -81
Du kannst, nun durch negative Zahlen dividieren, indem du die Division auf eine Multiplikation mit dem Kehrwert des Divisors zurückführst.
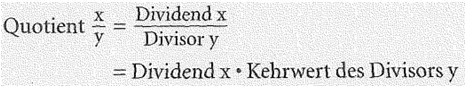
Beispiel:

Der Quotient aus Dividend und Divisor ist gleich dem Produkt aus Dividend und Kehrwert des Divisors, in Zeichen:
![]()
# Der Divisor y darf nicht Null sein!
Du weißt aus der Bruchrechnung, dass Dividend und Divisor nicht vertauscht werden dürfen. Für die Division gilt das Kommutativgesetz nicht! Auch das Assoziativgesetz darf nicht auf die Division angewendet werden.
Beispiel:
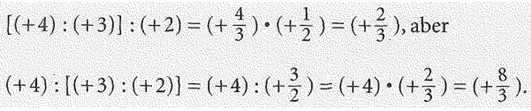
Hier eine Zusammenfassung.
Zu jeder Zahl aus Q existiert ein Kehrwert. Das Produkt aus Zahl und Kehrwert ist ( +1). Die Multiplikation ist kommutativ und assoziativ. Die Multiplikation mit (+1) ändert am
Produkt nichts. Die Multiplikation mit (-1) ändert dagegen das Vorzeichen des Produkts. Die Division in Q ist als Multiplikation mit dem Kehrwert des Divisors definiert. Der Divisor darf nicht gleich 0 sein. Für die Division gelten das Kommutativ- und das Assoziativgesetz nicht.
Übung:
Berechne. Wan die periodische Dezimalbrüche in gewöhnliche Brüche um.
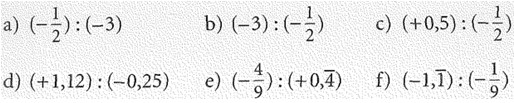
Lösung:
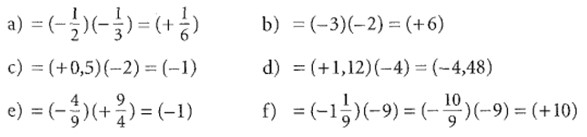
Übung:
Berechne
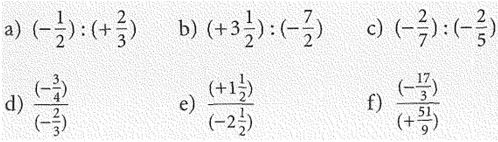
Lösung:
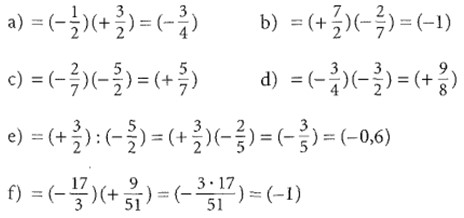
# Hinweis:
Der Doppelpunkt der Division kann durch einen Bruchstrich ersetzt werden. So können Doppelbrüche entstehen.
Übung:
Berechne in der folgenden Übung Zähler und Nenner einzeln und dann den Quotienten. Beachte die Klammerregeln.
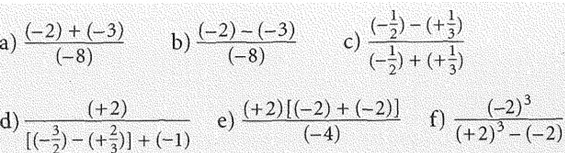
Lösung:
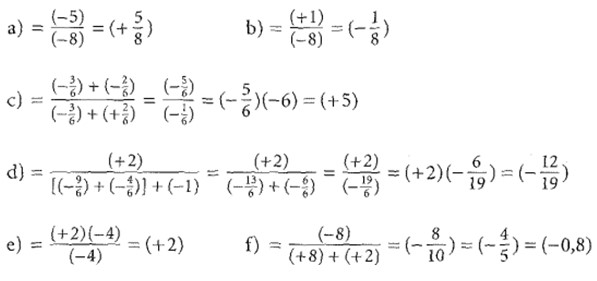
Bearbeite nun die Klassenarbeit Nr. 2. Du findest sie auf Seite 75. Lies zuvor die Seiten 72 und 73 genau durch.
Das folgende Beispiel zeigt, wie du kompliziertere Aufgaben löst.
Beispiel:

Übung:
Berechne die folgenden Quotienten.
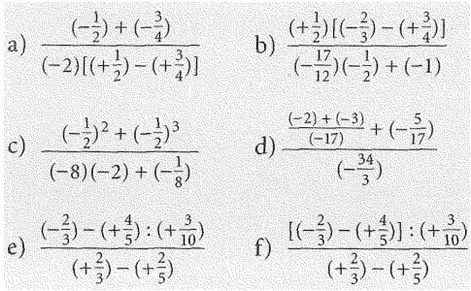
Lösung:
Dividend und Divisor sind hier nicht getrennt berechnet worden.