Auflösen (Weglassen) von Klammern: Steht ein Pluszeichen oder kein Vorzeichen vor der Klammer, darf man die Klammer einfach weglassen:
a + (b + c) = a + b + c
Steht ein Minuszeichen vor der Klammer, müssen die Vorzeichen in der Klammer geändert werden, wenn man die Klammer weglässt:
a-(b + c) = a- b- c

„Vorfahrtsregeln“ in Termen (T Kap. 1.5): Klammern werden zuerst berechnet. Bei geschachtelten
-Klammern wird die innere zuerst berechnet.
– Potenzrechnung wird vor Punkt- und Strichrechnung ausgeführt.
– Punktrechnungen (• und 🙂 werden vor Strichrechnungen ( + und -) ausgeführt.
Merke dir: Klam-Po-Pun-Stri

– Strich- und Punktrechnungen sind untereinander jeweils gleichrangig. Fehlen Klammern, rechnet man von links nach rechts.

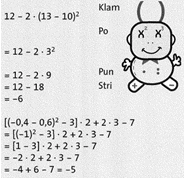
Als Platzhalter für Zahlen werden Variablen verwendet.

Je nachdem, welche Zahl du für die Variable einsetzt, nimmt der Term verschiedene Werte an.

Terme mit Variablen können ganz normal umgeformt bzw. vereinfacht werden.
Es gelten die bekannten Rechen- und Vorfahrtsregeln.

Searhie, Nur gleiche Variablen dürfen zusammengefasst werden.

Übung 24 Berechne die Terme. Hinweis: Löse zuerst die Klammern auf.

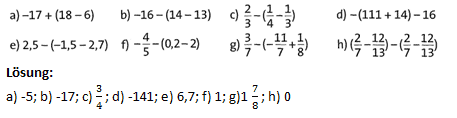
Übung 25 Welche der folgenden Terme haben den gleichen Wert? Berechne.

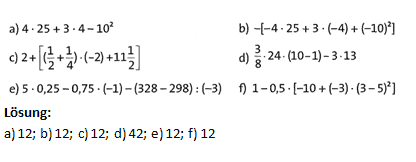
Übung 26 a) Setze in jeden der gegebenen Terme für die Variable x nacheinander die Zahlen aus der ersten Spalte ein und berechne die Werte.

b) Vereinfache die Ausgangsterme, indem du jeweils so weit wie möglich zusammenfasst.
c) Setze nun in jeden der vereinfachten Terme nacheinander die Zahlen für die Variable ein. Was stellst du fest? Warum ist das so?

Lösung:
a) und b) Die vereinfachten Terme stehen in der Kopfzeile.

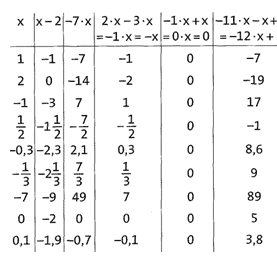
c) Das Einsetzen in die vereinfachten Terme liefert die gleichen Werte, allerdings mit weniger Rechenaufwand.

Übung 27 Kevin hat hier ganz schön schlampig gerechnet. In jeder seiner Rechnungen stecken zwei Fehler. Streiche die Fehler an und berechne richtig.

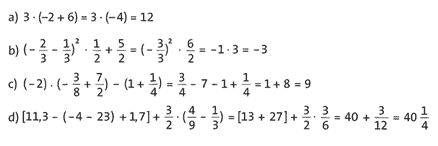
a) richtig: 3 • (-2 + 6) = 3 • 4 = 12;
und mit dem ersten Fehler weitergerechnet würde sich 3 • (-4) = -12 ergeben.

Übung 28 Übertrage jede der Aussagen zunächst in einen Term und berechne anschließend das Ergebnis. Nutze Rechenvorteile.

Lösung : 

Übung 29 „Man nehme eine beliebige Zahl (außer der Null), verdopple sie, addiere 8, multipliziere die Summe mit 4, subtrahiere 32 und teile das Ganze schließlich durch die ursprüngliche Zahl.“

a) Probiere dieses „Rechen-Rezept” jeweils mit einer natürlichen Zahl, einer negativen ganzen Zahl, einer positiven sowie einer negativen Bruchzahl aus. Was stellst du fest?

b) Schreibe das „Rezept” auf, indem du für die gewählte Zahl die Variable x einsetzt. Vereinfache den Term so weit wie möglich, löse ihn auf und begründe damit das Ergebnis aus a).

Lösung:
a) Alle Rechnungen führen zu demselben Ergebnis, nämlich 8. b) [(x • 2 + 8) • 4 – 32] : x
Vereinfacht man diesen Term, so erhält man: (8 • x) : x = 8.

Übung 30 Wolf gang jammert: „Meine Güte, diese vielen Rechengesetze kann ich mir nie merken!“ Da meint Monika: „Wieso? Zu den Distributivgesetzen musst du dir doch nur eine einzige Gleichung merken: a • (b + c) = a • b + a • c. Alle anderen kannst du daraus mithilfe anderer Gesetze und Regeln ableiten.“ Diesen Tipp kannst du auch nutzen.

a) Was musst du für * einsetzen, damit die Gleichung stimmt:
2 • (6 – 3) = 2 • (6 + *) ?

b) Was musst du hier für * einsetzen, wenn a, b, c beliebige rationale Zahlen sind:
a • (b – c) = a • (b + *) ?

c) Was musst du für * einsetzen, damit die Gleichung stimmt:

(7 + 3): 2 = (7 + 3) • * ?

d) Und allgemein: (a + b): c = (a + b) • * ? (c ≠ 0)

Lösung: