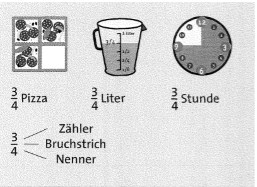
Ein Bruch steht für einen Anteil an einem Ganzen. Der Nenner gibt an, in wie viele gleich große Teile das Ganze aufgeteiit wird. Der Zähler gibt an, wie viele dieser Teile vorhanden sind.
Im Nenner eines Bruchs darf nie Null stehen!
Ist der Zähler eines Bruchs null, so ist der Wert des Bruchs gleich null.
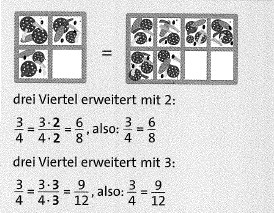
Ein Bruch wird erweitert, indem man seinen Zähler und seinen Nenner mit derselben Zahl (ungleich null) multipliziert.Der Anteil, für den der Bruch steht, ändert sich beim Erweitern nicht.Man sagt: Der Wert eines Bruchs bleibt beim Erweitern erselbe.
Ein Bruch wird gekürzt, indem man seinen Zähler und seinen Nenner durch dieselbe Zahl (ungleich null) dividiert. Der Wert des Bruchs bleibt derselbe.
Ein Bruch wird gekürzt, indem man seinen Zähler und seinen Nenner durch dieselbe Zahl (ungleich null) dividiert. Der Wert des Bruchs bleibt derselbe.

Wenn zwei Brüche denselben Wert haben, darf zwischen ihnen das Gleichheitszeichen (=) stehen.
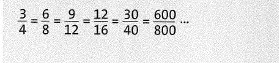
Wenn zwei Brüche denselben Wert haben, darf zwischen ihnen das Gleichheitszeichen (=) stehen.

Vergleichen von Brüchen
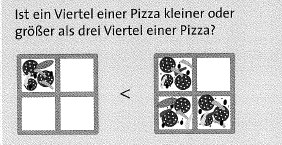
Brüche werden verglichen, um herauszufinden, welcher Bruch den größeren Wert hat. Wie bei den natürlichen Zahlen benutzt man die Zeichen < (kleiner als) und > (größer als).
Brüche mit gleichen Nennern heißen gleichnamig.Brüche mit verschiedenen Nennern heißen ungleichnamig.

Bei gleichnamigen Brüchen vergleicht man die Zähler. Der Bruch mit dem größeren Zähler hat den größeren Wert.

Ungleichnamige Brüche kann man auf einen gemeinsamen Nenner erweitern.
Man sagt: gleichnamig machen.
Als gemeinsamer Nenner kommen viele Zahlen in Frage.

Um ungleichnamige Brüche vergleichen zu können, muss man sie zuerst gleichnamig machen. Dann vergleicht man die Zähler.

Erweiterung auf den Hauptnenner
Der Hauptnenner zweier Brüche ist das kleinste gemeinsame Vielfache der Nenner. Dies wird kurz als das kgV der beiden Nenner bezeichnet. Man sagt: Auf den Hauptnenner erweitern.

Übung 1 Schreibe die abgebildeten Anteile jeweils als Bruch. Überlege, in wie viele Teile die Pizza aufgeteilt wurde und wie viele davon jeweils noch zu sehen sind. Prüfe auch, ob man noch kürzen kann.

Lösung 1
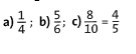
Übung 2 Die Brüche sollen wie angegeben erweitert beziehungsweise gekürzt werden. Ergänze die Lücken entsprechend.

Lösung 2
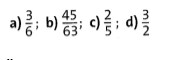
Übung 3 Erweitere die Brüche auf den Nenner 60. Du kannst dabei in einem Schritt erweitern oder in mehreren.

WİSSEN
Kürzen mit dem ggT
Manche Brüche kann man mehrfach kürzen. Mit dem größten gemeinsamen Teiler (ggT) von Zähler und Nenner kann man den Bruch auf einmal vollständig kürzen.Den ggT findest du folgendermaßen:
- Liste alle Teiler von Zähler und Nenner auf.
- Suche den größten gemeinsamen Teiler.

ÜBUNG 4 Kürze die Brüche so weit wie möglich.
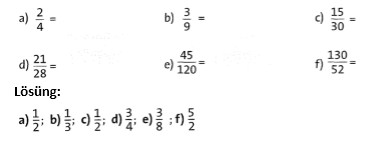
WİSSEN
Wie findet man das kgV zweier Zahlen?
1. Liste die ersten Vielfachen der größeren Zahl auf.
2. Schreibe die ersten Vielfachen der kleineren Zahl daneben.
3. Überprüfe der Reihe nach, ob eine Zahl der ersten Liste in der zweiten Liste auftaucht.Die erste Zahl, bei der du eine Übereinstimmung feststellst, ist das kgV.
4. Findest du keine Übereinstimmung, musst du die Listen verlängern und erneut ergleichen.

Übung 5 Bestimme das kgV der beiden Zahlen.
a) kgV (5,6)= b) kgV (4,6) = c) kgV (6,9)= d) kgV (12,18) =
Lösung:
a) 30; b) 12; c) 18; d) 36
Übung 6 Finde den Hauptnenner, erweitere beide Brüche auf den Hauptnenner und vergleiche sie miteinander. (Beachte, dass der Hauptnenner dem kgV der beiden Nenner entspricht!)
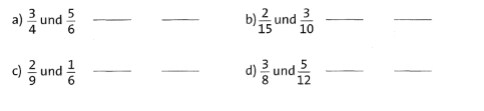
Lösung 6
![]()
Übung 7 Man kann auch das kleinste gemeinsame Vielfache von mehr als zwei Zahlen suchen. Gemeint ist damit die kleinste Zahl, die gleichzeitig ein Vielfaches aller gegebenen Zahlen ist. Finde das kleinste gemeinsame Vielfache der vier Zahlen 4, 5,6 und 8.
Lösung:
kgV(4, 5, 6, 8) = 120