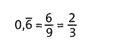Verwandlung einer endlichen Dezimalzahl in einen Bruch:
– Der Zähler ist die Dezimalzahl ohne Komma geschrieben.
– Der Nenner ist eine Zehnerpotenz (Stufenzahl), die genau so viele Nullen hat wie die Dezimalzahl Nachkommastellen.

Verwandlung eines Bruchs in eine endliche Dezimalzahl:
Lässt sich ein Bruch so erweitern oder kürzen, dass im Nenner eine Zehnerpotenz steht, so kann man ihn umwandeln, indem man zunächst auf die Zehnerpotenz erweitert oder kürzt und das Ergebnis anschließend als Dezimalzahl schreibt.
Ein Bruch kann auch mithilfe einer Division in die Dezimalschreibweise umgewandelt werden.

Periodische Dezimalzahlen

Manche Bruchzahlen können nicht so erweitert oder gekürzt werden, dass im Nenner eine Zehnerpotenz steht. Bei diesen Bruchzahlen bricht die Division auch an keiner Stelle ab. Die Ergebnisse wiederholen sich im Laufe der Rechnung. Solche Zahlen nennt man periodische Dezimalzahlen. Der periodische Teil wird durch einen Strich gekennzeichnet.

Die Periode tritt manchmal nicht sofort auf, sondern erst ab einer gewissen Stelle.Es kommt auch vor, dass sich bei der Division eine ganze Reihe von Ziffern wiederholt.

Die Anzahl der sich wiederholenden Ziffern heißt Länge der Periode.

Übung 23 Schreibe jede der Dezimalzahlen als Bruch. Wandle zuerst in einen Zehnerbruch um und kürze falls möglich. Schreibe in dein Übungsheft.

a) 0,7 b) 0,35 c) 1,3                     d) 0,09                  e) 1,8
f) 50,25                g) 10,5                  h) 1,383               i) 1,26                   j) 2,001

Lösung:

Übung 24 Schreibe jeden der Brüche als Dezimalzahl.

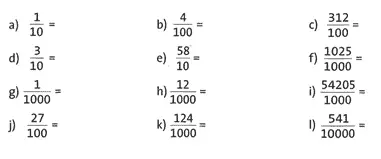
Lösung:
a) 0,1; b) 0,04; c) 3,12; d) 0,3; e) 5,8; f)l,025; g) 0,001; h) 0,012; i) 54,205; j) 0,27; k) 0,124; I) 0,0541

Übung 25 Erweitere jeden der Brüche zu einem Zehnerbruch. Schreibe anschließend jeweils als Dezimalzahl.

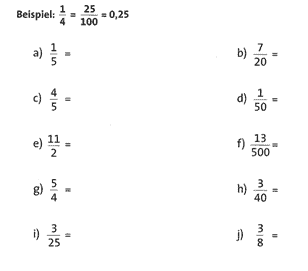
Lösung:
a) 0,2; b) 0,35; c) 0,8; d) 0,02; e) 5,5; f) 0,026; g) 1,25; h) 0,075; i) 0,12; j) 0,375

Übung 26 Verwandle jeden der Brüche durch Division in eine Dezimalzahl. Bei diesen Aufgaben geht die Division auf.

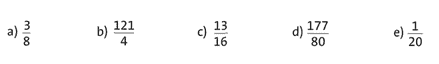
Lösung:
a) 0,375; b) 30,25; c) 0,8125; d) 2,2125; e) 0,05

Übung 27 Verwandle in die jeweils andere Schreibweise.

WİSSEN

Hilfreiche periodische Dezimalzahlen
Merkst du dir die folgenden periodischen Dezimalzahlen auswendig, so fallen dir Umrechnungen leichter:

Übung 28 Verwandle jeden der Brüche durch Division in eine Dezimalzahl.
Bei diesen Aufgaben liefert das Divisionsverfahren periodische Dezimalzahlen als Ergebnis. Gib jeweils auch die Periodenlänge an.

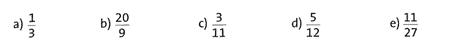
Lösung : 

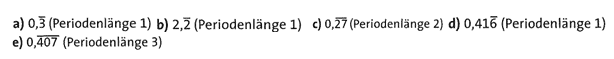
Übung 29 Ein Verein hat für ein Grillfest 400 Euro ausgegeben. Teilgenommen haben 10 Mitglieder und 10 Nichtmitglieder. Nichtmitglieder sollen in etwa das Doppelte zahlen wie Mitglieder. Mache einen Vorschlag, wie viel man von den jeweiligen Gästen verlangen soll, sodass die Kosten exakt wieder eingenommen werden.

Lösung:
Mitglieder zahlen 13,30 €. Nichtmitglieder zahlen 26,70 €.

Übung 30 Eine Mathematiklehrerin behauptet, sie könne jede beliebige periodische Dezimalzahl mit der Periodenlänge eins als Bruch schreiben.
Überprüfe das Ergebnis der unten stehenden Rechnung.
Übertrage die Rechnung auf die Zahl 0,6 und überprüfe dein Ergebnis.

Lösung :