Eine Bruchzahl kann man als Bruch oder in Dezimalschreibweise angeben. Man spricht auch kurz von Dezimalzahlen oder Dezimalbrüchen.

Die Stellen nach dem Komma heißen Nachkommastellen oder Dezimalen.

Die Stellenwerttafel des Zehnersystems wird um Zehntel, Hundertstel,Tausendstel usw. nach rechts fortgesetzt.

Die Stelle, an der eine Ziffer steht, bestimmt ihren Stellenwert.

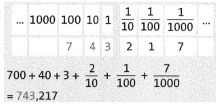
Den Wert einer Dezimalzahl erhält man, indem man jede Ziffer mit ihrem Stellenwert multipliziert und alle Teilergebnisse addiert.

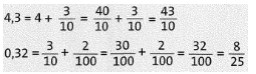
Jede Dezimalzahl hat einen eindeutigen Platz auf dem Zahlenstrahl.Für ein und dieselbe Zahl sind viele Schreibweisen möglich. Man schreibt normalerweise ohne Endnullen.

Von zwei Zahlen auf dem Zahlenstrahl ist immer die linke kleiner und die rechte größer.
Zwei Dezimalzahlen werden stellenweise von links nach rechts verglichen. Die größere Zahl ist diejenige, bei der zuerst eine größere Ziffer vorkommt.
Zur Vereinfachung können die Zahlen beim Vergleich stellenweise untereinander geschrieben werden.

Übung 1 Schreibe jeden der Zehnerbrüche (Brüche, deren Nenner Zehnerpotenzen sind) als Dezimalzahl.

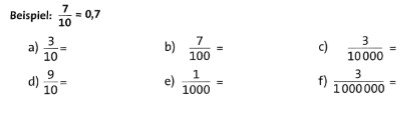
Lösung:
a) 0,3; b) 0,07; c) 0,0003; d) 0,9; e) 0,001; f) 0,000003

Übung 2 Schreibe die Dezimalzahlen mithilfe von Zehnerpotenzen und Zehnerbrüchen.

1,3 =

12,03 =

0,00102 =

Lösung:

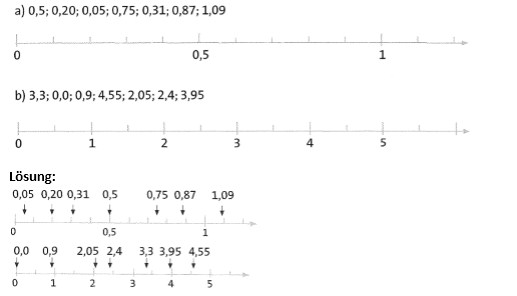
Übung 3 Trage die angegebenen Zahlen so genau wie möglich auf dem jeweiligen Zahlenstrahl ein. Benutze ein Lineal.

Übung 4 Schreibe jede der Dezimalzahlen zunächst als Zehnerbruch. Kürze falls möglich. Schreibe in dein Übungsheft.

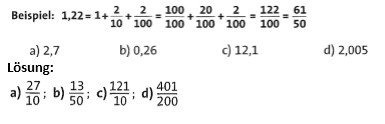
Übung 5 Ordne jedem der Brüche auf der linken Seite durch einen Pfeil die zugehörige Dezimalzahl auf der rechten Seite zu.

WİSSEN

Hilfreiche Dezimalzahlen auswendig wissen!

Beim Rechnen hilft es, wenn du die Schreibweisen für die folgenden Zahlen auswendig kennst:

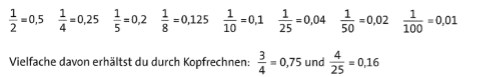
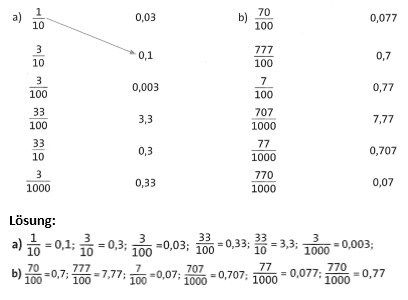
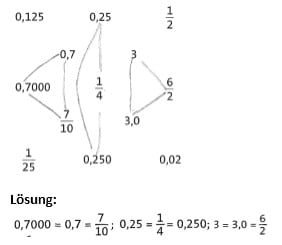
Übung 6 Wenn du die Zahlen, die denselben Wert haben, durch Linien verbindest, entsteht ein Muster. (Hinweis: Nicht zu allen Zahlen findest du eine Entsprechung!)

Übung 7 Lies die markierten Zahlen (a bis h) ab. Gib die Ergebnisse in Dezimalschreibweise an.

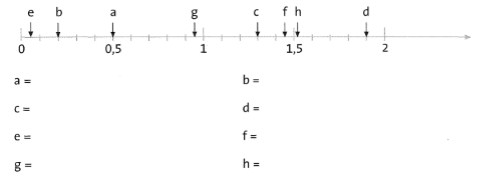
Lösung:
a = 0,5; b = 0,2; C = 1,3; d = 1,9; e = 0,05; f = 1,45; g = 0,95; h = 1,52
Übung 8 Sortiere die Dezimalzahlen der Größe nach.
12,3; 0,56; 0,123; 0,65; 0,8; 1,23; 1,22; 0,88
Lösung:
0,123 <0,56 <0,65 <0,8 <0,88 <1,22 < 1,23 < 12,3
Übung 9 Schreibe jeweils ohne Komma.
Beispiele: 1,2 kg = 1200 g; 22,42 m = 2 242 cm
a) 4,4 kg = b) 0,331 =
c) 12,3 dm = d) 22,031 =
e) 0,45 km = f) 1,3 cm2 =
g) 0,075 m = h) 0,82 m2 =
Lösung:
4400 g; 330 ml; 123 cm; 22 030 kg; 450 m; 130 mm2; 75 mm; 82 dm2
Übung 10 Vergleiche und trage in die Lücken <, > oder = ein:

Übung 11

Paul behauptet 2,1 Minuten entsprächen 210 Sekunden. Wie viele Sekunden sind es tatsächlich? Kannst du dir vorstellen, welchen Fehler Paul gemacht hat?

Lösung:
2,1min = 2min + 1/10 min = 120s + 6s = 126s
Tatsächlich entsprechen 2,1 Minuten 126 s.(Paul rechnet so, als ob eine Minute 100 Sekunden hätte.)