Wenn man eine Zahl durch eine andere Zahl teilt, so dividiert man diese Zahlen. Die Rechnung wird als Division bezeichnet. Wie es zu jeder Addition eine Subtraktionsaufgabe gibt, gibt es zu jeder Multiplikation eine Divisionsaufgabe.

Hauflig wird das Wort “Quotient” sowohl als Bezeichnung des Ausdrucks “12:3” als auch zur Bezeichnung seines Wertes “4” gebraucht.
Vorgehen beim schriftlichen Dividieren:
• Zerlege den Dividenden ziffernweise und dividiere anschließend,
• Screibe die Teilergebnisse stellenderecht untereinander.
• Anschließend wird subtrahiert, eine weitere Ziffer nach unten geholt und mit der Division fortgefahren.
Obige Division ist die Umkehrung der Multiplikation “3.4=12”. Die Richtigkeit einer Division kann durch die entsprechende Multiplikation überprüft werden.
Bei der schriftlichen Division werden Dividend und Divisor hintereinander geschrieben. Danach wird Schritt geprüft, wie oft der Divisior in den Dividenden “passt”.
Beispeile:
1. Dividiere schriftlich 608:8

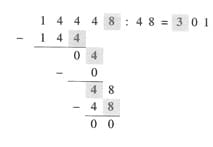
2. Die Division durch mehrstellige Zahlen ist schwerer: Dividiere 7 848 : 72.

Einige spezielle Divisionen lassen sich besonders einfach durchführen.
• Die Division durch 0 ist nicht erlaubt!
• 0 kann man aber durch jede Zahl (außer 0) dividieren. Das Ergebnis ist stets 0.
• Wenn du einen Dividenden durch 1 dividierst, so ist der Quotient gleich dem Dividenden selbst.
• Wenn Dividend und Divisor die gleiche Zahl sind, so ist der Quotient stets 1.
1. 45:0 = 45
2. 0:389 = 0 Probe 0.389=0
3. 128:1 = 128 Division mit 1 lässt die Zahl unverländert
4. 456:456 = 1 Division durch dieselbe Zahl ergibt immer 1.
5. 340:10 = 34 10 hat 1 Null -> Streiche 1 Nullen von der Zahl.
6. 56 700:100 = 567 100 hat 2 Nullen -> Streiche 2 Nullen von der Zahl.
7. 8 093 000:1 000 = 8 093 1 000 hat 3 Nullen –> Streiche 3 Nullen von der Zahl.

Wenn eine Division nicht “glatt” aufgeht, so ergibt sich ein Rest.

Beispeil :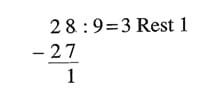

63. Dividiere (achte dabei auf den Rest) :
a) 348:6
b) 19:2
c) 367:8
d) 456:34
e) 9 768:22
f) 5 200:25
g) 58 941:41
h) 20 863:31
i) 7 888 028:0
j) 8 033 255:251

63. Lösungen :

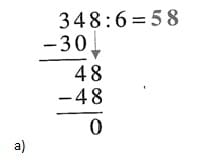
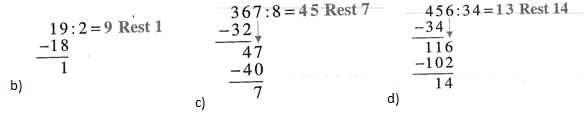
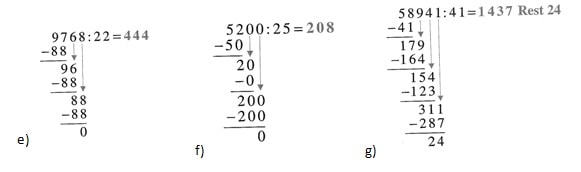
64. Welche Aufgaben sind falsch, welche sind richtig?
a) 943:23 = 41
b) 162:9 = 17 R:7
c) 18 036:17 = 106 R: 16
d) 1 401:9 = 157
e) 189:4 = 47 R: 1
f) 470:47 = 10
64. Lösungen :

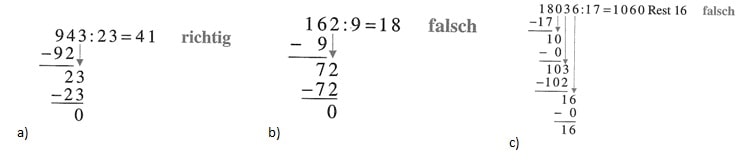
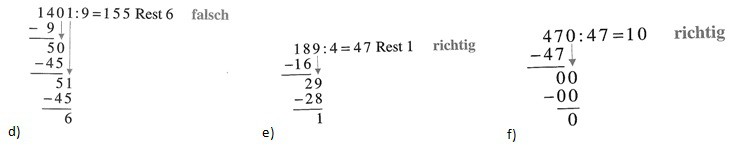
65. Rechne die Aufgaben und mache die Probe mit einer Umkehraufgabe.
a) 21 708:12
b) 3 901:9
c) 1 872:36
d) 48:7

65. Lösungen :

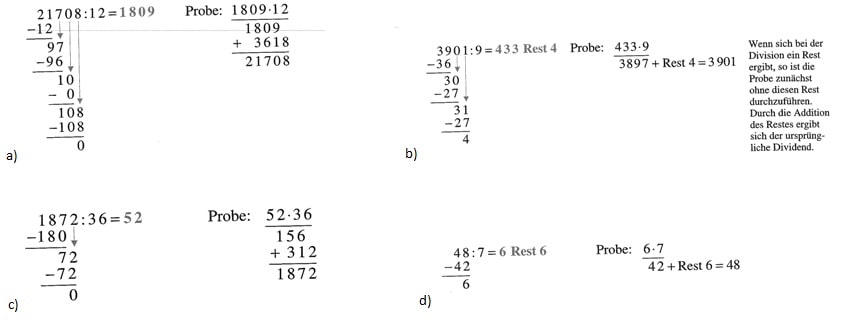
66. Ergänze die graunen Felder:

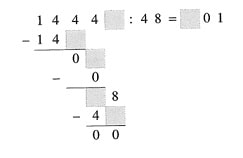
66. Lösungen :

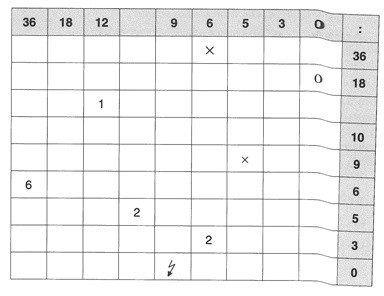
67. Erganze alle leeren Felder:
Wenn eine Aufgabe nicht ganzzalig aufgeht, so mache ein Kreuz (x).
Ist eine Aufgabe nicht definiert, so schreibe.
Dividend ist die graue Zeile, Divisior ist die graue Spalte. Die Ergebnisse der
Divisionen stehen in den weißen Feldern an den entsprechen den Kreuzungspunkten.
Wenn du alles ausgefüllt hast, betrachte das Schema noch mal in Ruhe.
Fällt dir etwas auf?

67. Lösungen :

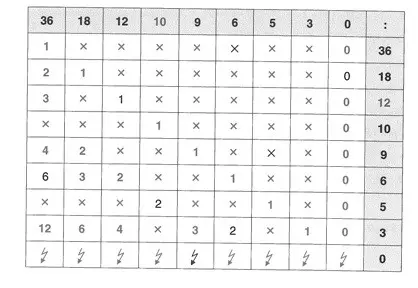
Es fällt auf, dass
• Die Division durch 0 immer “nicht definiert” ist
• 0 dividiert durch eine andere Zahl immer 0 ergibt (außer durch 0 selbst!).
• Eine Zahl dividiert durch sich selbst immer 1 ergibt (Ausnahme: 0).
• Die Zahl 36 die meisten Teiler hat(6) und die Zahlen 3 und 5 die wenigsten (1).
68.
a) Der Quotient beträgt 75:25.
Wie kann man Dividend und Divisor so verändern, dass sich der Wert des Quotienten nicht ändert?
b) Der Wert des Quotienten beträgt 5.
Welche Werte können der Dividend und der Divisor jeweils haben?
Gibt es mehrere Möglichkeiten?

68. Lösungen :
a) Der Wert des Quotienten änndert sich nicht, wenn Dividend und Divisor durch dieselbe Zahl dividiert werden, z. B. 5. Der Quotient heißt dann 15:5.
Der Wert des Quotienten ändert sich auch dann nicht, wenn Dividend und Divisor mit derselben Zahl multipliziert werden, z. B. 2. Der Quotient heißt dann 150:50.
b) 5:1=5
oder: 10:2 = 5
oder: 15:3 = 5
usw.
Aber auch 300:60=5, 15 000: 3 000 = 5, usw.
Es können alle Zahlenpaare genommen werden, bei denen der Dividend das 5-fache des Divisors beträgt.