Zwei Terme, die durch ein Gleichheitszeichen verbunden sind, bilden eine Gleichung.

2 + (-4) = 2 – 4

5 . x = -20

In einer Gleichung, die eine Variable (Unbekannte) enthält, kann man für die Variable Zahlen einsetzen. Dabei entsteht entweder eine wahre oder eine falsche Aussage.
Die Menge der Zahlen, die man in die Gleichung einsetzen darf, heißt Grund-menge G.

Die Zahlen aus der Grundmenge, welche die Gleichung beim Einsetzen zu einer wahren Aussage machen, heißen Lösungen dieser Gleichung.
Die Menge aller Lösungen einer Gleichung heißt Lösungsmenge L.
Wenn es zu einer Gleichung keine Zahl in der Grundmenge gibt, die diese Gleichung löst, ist die Lösungsmenge die leere Menge: L = {} bzw. 0

Es gibt mehrere Möglichkeiten, die Lösung einer Gleichung zu bestimmen:
– durch gezieltes Probieren;
– durch Überlegen;
– durch Umkehrungen (↑ nächste Seite).

Grundsätzlich solltest du anschließend eine Probe durchführen.

Probe : 3 . 4 + 20 = 32 ✓

Übung 31 Löse die Gleichungen durch Überlegen und gezieltes Probieren.

a) x + 4 = 23 b) 33 – x = 15                      c) x – 89,2 = 0                     d) 2 • x = 112

e) 2,5 • x = -10 f) x : 5 + 1 = 101                                g) 20 : x = 44 – 49             h) 20 + x = 99 + x – 79

Lösung:
a) L = {19}; b) L = {18}; c) L = {89,2}; d) L = {56}; e) L = {-4}; f) L = {500} g) L = {-4}; h) L =0,
also alle rationalen Zahlen.

Übung 32 Stelle eine Gleichung auf und bestimme die gesuchte Zahl.
a) Das Dreifache der gesuchten Zahl ergibt 54.
b) Das Doppelte einer Zahl ist -112.
c) Das Fünffache einer Zahl vermindert um 7 ergibt 8.
d) Wenn man 11 von dem Quadrat einer Zahl subtrahiert, erhält man 158.
e) Wenn man 1 zu einem Drittel der gesuchten Zahl addiert, erhält man -110.

Lösüng:
a) 3 • x = 54; L = {18}
b) 2 • x = -112; L = {-56}
c) 5 • x – 7 = 8; L = {3}
d) x2 – 11 = 158; L = {13}
e) 1 + x : 3 = -110; L = {-333}

Übung 33 Michael geht mit seinem Vater in den Zoo. Die Eintrittskarte des Vaters kostet dreimal so viel wie Michaels. Zusammen bezahlen sie 12 Euro.

a) Wie viel hat Michaels Eintrittskarte gekostet, wie viel die seines Vaters?
Stelle eine Gleichung auf und löse sie.

b) Am nächsten Wochenende gehen sie wieder in den Zoo, dieses Mal gehen auch Michaels Mutter und seine beiden Schwestern mit. Eine Familienkarte kostet 20 €. Lohnt es sich für die Familie, eine solche Karte zu kaufen?

Lösung:
a) x = Preis für Michaels Eintrittskarte;
3 • x + x = 12, L = {3}; also kostet Michaels Karte 3 €, die des Vaters 9 €.

b) 2 • 9 + 3 • 3 = 27; ja, es lohnt sich, eine Familienkarte zu nehmen, denn sie sparen mit der Familienkarte 7 €.

WİSSEN

Die wichtigsten Umkehrungen auf einen Blick
Merke dir die folgenden Umkehrungen oder jeweils ein Beispiel dazu, dann fallen dir Umformungen von Gleichungen leichter.

Übung 34 Die unten abgebildete Wippe befindet sich im Gleichgewicht. (Die kleinen Vögel wiegen alle gleich viel und die großen Vögel wiegen ebenfalls alle gleich viel.)

a) Bestimme durch geschicktes Wegstreichen das
Gewicht eines kleinen Vogels im Vergleich zu dem
eines großen Vogels. (Tipp: Du musst auf beiden
Seiten gleich viel wegnehmen, damit die Waage
im Gleichgewicht bleibt!)

b) Wie schwer ist ein kleiner Vogel, wenn ein großer Vogel 270 g wiegt?

Lösung:
a) Vier kleine Vögel wiegen so viel wie zwei große, also wiegt ein kleiner Vogel halb so viel wie ein großer,
b) Ein kleiner Vogel wiegt dann 135 g.

Übung 35 Gib jeweils zuerst die Grundmenge G an und bestimme anschließend die Lösungsmenge L.
Beispiel: Für welchen Teiler t der Zahl 12 gilt 12: t = 4? G = {1; 2; 3} und L = {3}, da 12 : 3

a) Für welche natürliche Zahl n gilt 8 • n + 50 = 74?
b) Für welchen Teiler t der Zahl 30 gilt: 5 • t + 25 = 50?
c) Welche ganze Zahl z erfüllt die Gleichung 2 • z -16 = -77 + 107?
d) Für welche Quadratzahl q gilt 12 • 12 + q = 13 • 13?

Lösung:

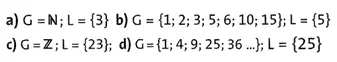
Übung 36 Lisa will mit einer Waage und Gewichten bestimmen, wie viel eine Dose wiegt. Leider sind die einzelnen Gewichte nicht beschriftet.

a) Bestimme durch Wegstreichen, wie viele Gewichte zusammen genau so viel wiegen wie die Dose. (Tipp: Du musst auf beiden Seiten gleich viel wegnehmen, damit die Waage im Gleichgewicht bleibt!)

b) Lisas Mutter weiß zum Glück noch, dass ein Gewicht 175 g wiegt. Wie schwer ist eine Dose demnach?

c) Übertrage das Problem in eine mathematische Gleichung, verwende die Variable d für das Gewicht einer Dose.

d) Bestimme die Lösung der Gleichung aus c) und vergleiche mit dem Ergebnis aus a). Führe eine Probe durch!

e) Wie schwer wäre eine Dose, wenn ein Gewicht 120 g schwer wäre?

Lösung:
a) 2 Dosen wiegen soviel wie 4 Gewichte, also wiegt eine Dose so viel wie 2 Gewichte.

b) Eine Dose wiegt 350 g.

c) 2 d + 3 • 175 = 7 • 175. d) L = {350} e) Eine Dose wiegt dann 240 g.

Übung 37 Carsten hat zu Weihnachten ein Handy mit Vertrag bekommen. Seine monatliche Handyrechnung setzt sich zusammen aus einer Grundgebühr von 10 € sowie den Kosten für die Gesprächszeit in Höhe von 40 ct pro Minute.

a) Wie viel muss Carsten zahlen, wenn er im Monat 27 Minuten telefoniert hat?

b) Nach dem zweiten Monat muss er einen Rechnungsbetrag in Höhe von 40,40 € zahlen. Wie lange hat er dafür telefoniert?

c) Sein Bruder Holger hat ein Handy mit einem anderen Vertrag. Er zahlt keine Grundgebühr, dafür kostet eine Gesprächsminute 50 ct. Wäre dieser Vertrag günstiger bei 76 Gesprächsminuten?

d) Jetzt will Carsten vergleichen, wie lange er und sein Bruder telefonieren müssten, um genau den gleichen Rechnungsbetrag zu erzielen. Kannst du ihm bei dieser schwierigen Aufgabe helfen? Untersuche die Fälle, wenn beide entweder gleich lang telefonieren oder Carsten gar nicht telefoniertl Dabei kannst du die Rechnungsbeträge durch einen Term mit einer Variablen berechnen. Beide Rechnungsbeträge müssen jetzt gleich sein, stelle also eine Gleichung auf.
Finde die Lösung und führe eine Probe durch.

Lösung:
Rechnungen ohne Einheiten:

a) 27 • 0,40 + 10 = 20,80; Carsten muss 20,80 € zahlen.

b) x • 0,40 + 10 = 40,40: L = {76}; Carsten hat also 76 Minuten telefoniert.

c) 76 • 0,50 = 38; Holger zahlt nur 38 € und damit weniger als Carsten.

d) x • 0,40 + 10 = X • 0,50; L = {100};
wenn jeder 100 Minuten telefoniert, müssen beide den gleichen Betrag zahlen;
10 = x • 0,50; L = {20};
wenn Carsten gar nicht telefoniert, zahlt er trotzdem 10,- €. Dafür kann Holger 20 Minuten telefonieren.