Anhand dieser berühmten Schacbrettaufgabe lässt sich die Nützlichkeit der Potenzschreibweise gut nachvollziehen: Der Erfinder des Schachspeils sollte von seinem König für seine Erfindung belohnt werden. Er verlangte “nur” Folgendes : für das 1.Feld 1 Reiskorn, für das 2. Feld 2 Reiskörner, für das 3.Feld 4 Reiskörner, für das 4. Feld 8 Reiskörner usw. Für jedes weitere Feld bedeutete dies eine Verdopplung (.2) der vorhergehenden Reiszahl.
Das Bild zeigt die ersten 7 felder:

Man erkennt: Die wachsende Anzahl der Reiskörner kann man als Multiplikation mit dem immer gleichen Faktor 2 auffassen.
Übrigens: Es gibt nicht genug Reiskörner auf der Welt, um alle 64 Felder eines Schachbretts nach dieser Methode zu belegen!
Für die Multiplikation mit gleichen Faktoren gibt es eine Kurzschreibweise, damit die Rechnungen nicht zu lange werden.
Der Rechenausdruck ab heißt Potenz und bedeutet:
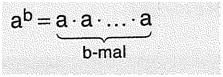
Dabei ist a die Grudzahl und b die Hochzahl.
Es gilt:
• Potenzen mit der Grundzahl 1 ergeben immer die 1 selbst : 1b = 1
• Potenzen mit Hochzahl 1 ergeben immer die Grundzahl selbst: a1 = a
• Potenzen mit der Hochzahl 0 ergeben immer die 1: a0 = 1
Beispeile:
1. Schreibe 15 und 91 jeweils als Produkt und berechne.
Lösungen :
15 = 1.1.1.1.1 = 1 und 91 = 9
2. Schreibe 7.7.7.7 als Potenz und berechne.
Lösungen :
7.7.7.7 = 74 = 2 401
3. Vergleiche 62 und 26
Lösungen :
62 = 6.6 = 36 und 26 = 2.2.2.2.2.2 = 64
• Potenzen mit der Hochzahl 2 heißen Quadratzahlen.
• Potenzen mit der Hochzahl 3 heißen Kubikzahlen.
• Potenzen mit der Grundzahl 10 heißen Zehnerpotenzen.
Bei Zehnerpotenzen gibt die Hochzahl die Anzahl der Nullen an.
Beispeile: 1. Welche Potenz verbirgt sich hinter der Zahl 81?
Lösungen :
81 = 92 oder 34
2. Schreibe 10 000 000 als Zehnerpotenz.
Lösungen :
10 000 000 = 107
Bei zehnerpotenzen ist die Hochzahl gleich der Anzahl der Nullen.
77. Beispeil : . Eine Alle ist 300 m Lang. Die Bäume stehen in einem Abstand von 10 m. Wie viele Bäume hat die Allee? (Vernachlässige bei der Berechnung die Dicke der Bäume.)
Mithilfe der informativen Figur erkennt man (oder zählt einfach ab), dass auf jeder Seite der Allee 31 Bäume stehen.
Es sind demnach also 31•2 = 62 Bäume.
oder:
Wenn die Bäume an einer Allee in einem Ab¬stand von 10 m stehen, so kann man dies mit einer Gleichung ausdrücken:
Ein 10-m-Abstand passt in 300 m genau
a) mal. Bei x Abständen muss es x + 1 Bäume auf jeder Seite geben.
Gleichung: 2 • (30 +1) = 62 Bäume
Bei Aufgaben, in denen der Umwelt¬bezug eine Rolle spielt, hilft dir meis¬tens entweder eine informative Figur, eine Gleichung oder eine Tabelle, die Aufgabe so vorzubereiten, dass du sie leichter lösen kannst.
78. Beispeil : Während einer Vertretungsstunde sollten die Schüler der 5. Klasse herausfinden, wie oft die Ziffer 1 in den Seitenzahlen ihres Mathematikbuchs vorkommt. Das Buch hat 209 Seiten. Kann man die Lösung finden, ohne das Buch einzeln durchzublättern und die Zahl 1 immer wieder aufzuschreiben?
78. Lösungen :
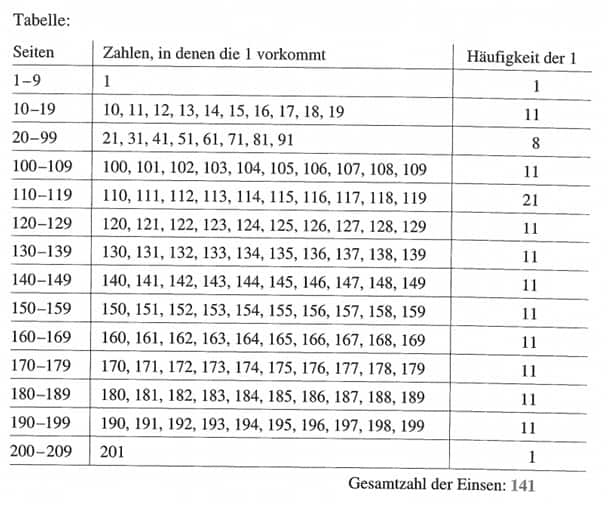
oder:
In den Seitenbereichen 10-19, 100-109,120-129, 130-139, 140-149, 150-159,160-169, 170-179,
180-189, 190-199 kommt die Zahl 1 jeweils 11-mal vor.
Also insgesamt 10-11-mal = 110-mal.
In den Seitenbereichen 1-9, 20-99, 110-119 und 200-209 muss man abzählen:
1-mal,8-mal, 21-mal und 1-mal ergibt zusätzlich: 31-mal
Gleichung: 10 • 11 + 1 + 8-1-21 + 1 = 110-1-31 = 141 Man kann die Lösung also auch herausfinden, ohne das Buch durchzublättem.
Bei Aufgaben, in denen der Umweltbezug eine Rolle spielt, hilft dir meistens entweder eine informative Figur, eine Gleichung oder eine Tabelle, die Aufgabe so vorzubereiten, dass du sie leichter lösen kannst.
79. Beispeil :Schaue die folgenden Aufgaben genau an, bevor du rechnest.
a) 15.(15-15)+15
b) (34:2+45.21).0
c) 45+34:17-45
d) (20+4.0).(78-77)
e) 4:(789-785)
f) 1 205:[34:(68:2)]
79. Lösungen :
a)15 • (15 — 15) + 15 = 15 • 0+ 15 = 0 + 15 = 15 Multiplikation mit 0 ergibt 0.
b)(34 : 2 + 45 . 21) • 0 = 0 Multiplikation mit 0 ergibt 0, auch wenn es sich um einen komplizier¬ten Rechenausdruck handelt.
c)45 + 34: 17 — 45 = 45 — 45 + 34: 17 = 0 + 2 = 2 Anwendung des Kommutativ¬ gesetzes
d)(20 + 4 • 0) • (78 — 77) = (20 + 0) • 1 =20 • 1 =20 Punkt vor Strich in der ersten Klammer
e)4 : (789 —785) = 4 : 4= 1 Klammer zuerst
f)1 205 : [34: (68 :2)] = 1 205: [34:34] = 1 205 :1 = 1205 Klammem zuerst
80. Beispeil :
a) Addiere zur Summe der Zahlen 4 und 8 die Differenz der Zahlen 40 und 35.
b) Subtrahiere von der Differenz der Zahlen 40 und 30 die Summe der Zahlen 2 und 3.
c) Addiere zum Produkt der Zahlen 4 und 5 den Quotienten der Zahlen 10 und 5.
d) Bilde den Quotienten aus der Summe von 4 und 6 und der Differenz der Zahlen 8 und
80. Lösungen :
a) (4 + 8) + (40 — 35)= 12 + 5 = 17
b) (40 — 30) — (2+ 3) = 10 — 5 = 5
c) (4 • 5) + (10 : 5) = 20+ 2 = 22
d) (4 + 6): (8 – 3) = 10:5 = 2
81. Beispeil : Schreibe folgende Rechenausdrücke in Worten.
a) (8-6).5
b) 8-6.5
c) (4+3).(4-3)
d) 4+3.4-3
81. Lösungen :
a) Multipliziere die Differenz der Zahlen 8 und 6 mit der Zahl 5. oder:
Bilde das Produkt aus der Differenz der Zahlen 8 und 6 und der Zahl 5.
b) Subtrahiere das Produkt der Zahlen 6 und 5 von 8. oder:
Bilde die Differenz aus 8 und dem Produkt der Zahlen 6 und 5.
c) Multipliziere die Summe von 4 und 3 mit der Differenz von 4 und 3. oder:
Bilde das Produkt der Summe von 4 und 3 und der Differenz von 4 und 3.
d) Subtrahiere die Zahl 3 von der Summe von 4 und dem Produkt aus 3 und 4. oder:
Bilde die Differenz aus der Summe von 4 und dem Produkt aus 3
82. Beispeil : Für eine Theateraufführung des Schultheaters hat die Schule eine bestimmte Anzahl von Stühlen im Keller. Der Hausmeister überlegt, dass 12 Reihen mit je 20 Stühlen möglich wären.
Wie viele Reihen würden entstehen, wenn in jeder Reihe 15 Stühle wären?
82. Lösungen :
Jede der 12 Reihen hat 20 Stühle, also gibt es insgesamt 12 • 20 = 240 Stühle. Bei 15 Stühlen pro Reihe erhält man die Anzahl der benö¬tigten Reihen, indem man die Anzahl der Stühle durch die Anzahl der Stühle pro Reihe dividiert. Das Ergebnis lautet:
240:15 = 16 Reihen.
Informative Figur:
83. Beispeil : Jennifer sagt: Ich denke mir eine Zahl, teile sie durch 6, multipliziere dann mit 2 und erhalte 50.
An welche Zahl hat sie gedacht?
83. Lösungen :
Diese Aufgabe ist „rückwärts“ zu lösen: Wenn man zuerst durch 6 dividiert und dann mit 2 multipli-ziert, erhält man 50. Das heißt, du musst umgekehrt erst die Zahl 50 durch 2 dividieren und anschlie-ßend mit 6 multiplizieren.
Rechnung:
50:2-6 = 25-6 = 150
Jennifer hat an die Zahl 150 gedacht.
84. Beispeil : Eine Kunstausstellung dauerte 5 Wochen. In der letzten Woche kamen 1 296 Besucher. In den beiden vorhergehenden Wochen kamen jeweils gleich viel Besucher. In der 1. Woche kamen 1 205 Besucher. In der 2. Woche waren es 155 mehr. Insgesamt waren es 6 045 Kunstinteressierte.
Mit diesen Daten lässt sich eine Vielzahl von Fragestellungen beantworten:
a) Wie viele esucher kamen in der 2. Woche?
b) Wie viele Besucher kamen in der 3. Woche?
c) In welcher Woche kamen die meisten Besucher?
d) In welcher Woche kamen die wenigsten Besucher?
e) Angenommen, es kämen in jeder Woche gleich viele Besucher. Wie viele wären es dann pro Woche?
f) Wie viele Besucher kämen, wenn die Ausstellung 12 Wochen dauern würde und der Zuspruch genauso groß wie in den ersten 5 Wochen bliebe?
84. Lösungen :
a) In der 1. Woche kamen 1 205 Besucher.
In der 2. Woche waren es 155 Besucher mehr.
Rechnung: 1 205 +155 = 1 360
In der 2. Woche kamen 1360 Besucher.
b) 1. Woche: 1 205 Besucher
2. Woche: 1 360 Besucher
3. Woche: gleich viele Besucher wie in der 4. Woche
4. Woche: gleich viele Besucher wie in der 3. Woche
5. Woche: 1 296 Besucher
Gesamt: 6045 Besucher
Rechnung:
6045-1205-1360-1296 = 2184
Rechnung:
2184:2=1092
In der 3. Woche kamen 1 092 Besucher.
c) In der 2, Woche kamen mit 1 360 Personen die meisten Besucher.
d) In der 3. und 4. Woche kamen die wenigsten Besucher, nämlich nur 1 092 Personen.
e) Rechnung: 6 045:5 = 1 209
Es wären dann 1209 Besucher pro Woche.
f) Rechnung: 1 209 • 12= 14 508
In 12 Wochen kämen I Besucher.
Für die Besucherzahl in der 3. und 4. Woche werden von der Gesamtbesucherzahl die Besucherzahlen der 1., 2. und 5. Woche subtrahiert. Da in der 3. und 4. Woche gleich viele Besucher kamen, ist die er-rechnete Besucherzahl noch durch 2 zu teilen.
Die Gesamtzahl aller Besucher beträgt 6 045 Personen. Wenn in jeder der 5 Wochen gleich viele
Besucher gekommen wären, müsste man die Gesamtzahl durch 5 dividieren.
Wenn in jeder Woche 1 209 Besucher gekommen wären, wären in 12 Wochen 12-mal so viele Besucher gekommen.