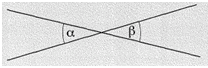
Die beiden gegenüberliegenden Winkel an zwei sich schneidenden Geraden heißen Scheitelwinkel. Scheitelwinkel sind gleich groß.

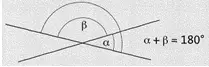
Nebeneinander liegende Winkel an zwei sich schneidenden Geraden heißen Nebenwinkel. Nebenwinkel ergeben zusammen 180°.

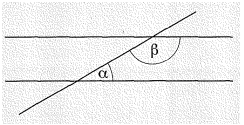
Schneidet eine Gerade zwei andere Geraden, so entstehen Stufenwinkel. Stufenwinkel an Parallelen sind gleich groß.

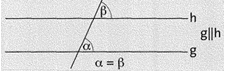
Wechselwinkel liegen auf verschiedenen Seiten von g und h. Man nennt sie auch Z-Winkel. Wechselwinkel an Parallelen sind gleich groß.

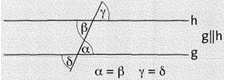
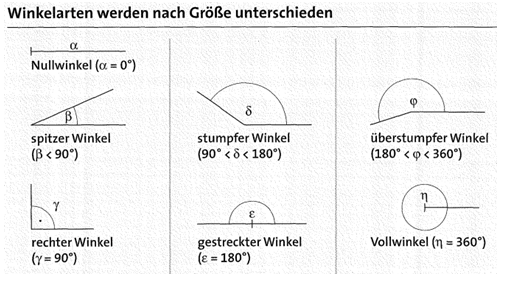
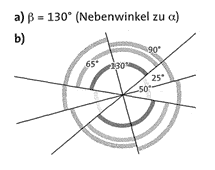
Übung 9 Gib zu jedem Winkel die Winkelart an. (Beispiel: spitzer Winkel, stumpfer Winkel usw.)

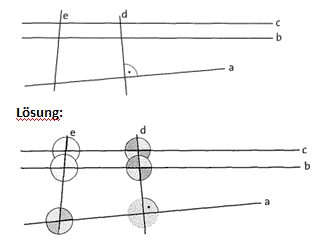
Lösung:

Übung 10 Zeichne zu 8 jeweils die angegebenen Winkel ein (es sind mehrere Lösungen möglich). Die Geraden g und h sind parallel.

a)

Übung 11 Färbe gleich große Winkel in der gleichen Farbe. Die Geraden b und c sind parallel. Die Gerade a steht senkrecht auf d.

Übung 12 Wie groß sind a und ß, wenn

 

Übung 13 Welchen Winkel überstreicht der Minutenzeiger in den angegebenen Zeiträumen? (Tipp: Überlege dir, welchen Winkel der Minutenzeiger in einer Minute überstreicht.)
a) 12.00 Uhr bis 12.20 Uhr
b) 12.54 Uhr bis 13.07 Uhr
c) 23.11 Uhr bis 0.33 Uhr
d) 10.30 Uhr bis 13.00 Uhr

Lösung:
In einer Minute überstreicht der Minutenzeiger einen Winkel von 360° : 60 = 6°.
a) 120° (= 20 • 6°)
b) 78° (= 13 • 6°)
c) 492° (= 82 • 6°)
d) 900° (= 150 • 6°)

WİSSEN

Winkelhalbierende
Eine Gerade, die einen Winkel halbiert,heißt
Winkelhalbierende.
Schneiden sich zwei Geraden, so können wir zwei Winkelhalbierende einzeichnen.

An einer solchen Geradenkreuzung stehen die beiden Winkelhalbierenden senkrecht aufeinander.

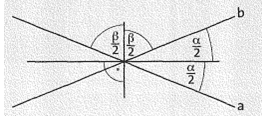
Übung 14 Betrachte die Zeichnung im Kasten. Es sei a = 50°.
a) Wie groß ist dann ß? Begründe deine Antwort.
b) Übertrage die Zeichnung mit Winkel a = 50° in dein Übungsheft. Bestimme zunächst alle weiteren Winkel, überprüfe anschließend durch Messen.

Lösung:

Übung 15 Wie groß sind jeweils a, ß und y ? Begründe.
a) Die Geraden a und b sind parallel,
b) Die Gerade a halbiert den rechten c und d bilden einen rechten Winkel. Winkel, der von c und d gebildet wir

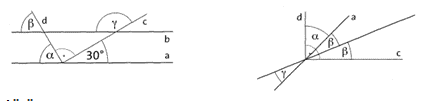
Lösung:

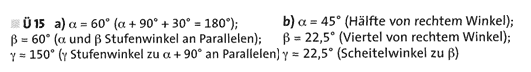
WİSSEN

Nachbarwinkel

Entgegengesetzt liegende Winkel, wie a und ß in dieser Zeichnung, nennt man auch Nachbarwinkel. Nachbarwinkel an Parallelen ergänzen sich zu 180°.

Übung 16 Betrachte die Zeichnung im Kasten. Begründe, wieso Nachbarwinkel an Parallelen zusammen 180° ergeben. Nutze dafür deine Kenntnisse über Winkel an Parallelen.

Lösung:
ß ist der Nebenwinkel zum Stufenwinkel von a. Da die Geraden parallel sind, ist dieser Stufenwinkel genau so groß wie a, und damit gilt a + ß = 180°.