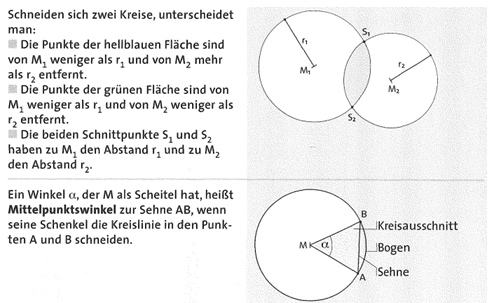
Alle Punkte, die von einem Punkt M den gleichen Abstand r haben, liegen auf einem Kreis (einer Kreislinie). M heißt
Mittelpunkt, r heißt Radius des Kreises.

Jede Verbindungsstrecke zwischen einem Punkt P der Kreislinie und M heißt ebenfalls Radius r des Kreises. Ein
Kreis um M mit dem Radius r wird mit K(M; r) bezeichnet.

Alle Punkte I, deren Abstand zu M kleiner ist als r, liegen innerhalb (im Inneren) des Kreises. Alle Punkte A, deren Abstand zu M größer ist als r, liegen außerhalb des Kreises.

Jede Verbindungsstrecke von zwei Punkten der Kreislinie heißt Sehne S. Jede Sehne, die durch M verläuft, heißt Durchmesser d. Es gilt: d = 2 • r.

Übung 17 Zeichne in dein Übungsheft
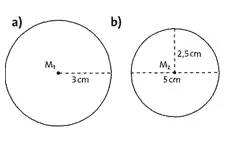
a) einen Kreis um einen Mittelpunkt M1 mit dem Radius r = 3 cm.
b) einen Kreis mit dem Durchmesser d = 5 cm um einen Mittelpunkt M₂.

Lösung:

Übung 18 Zeichne in dein Übungsheft.
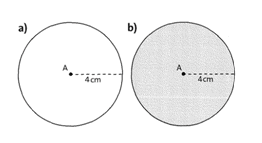
a) Wo liegen alle Punkte, die von einem Punkt A den Abstand 4 cm haben? Zeichne.
b) Färbe den Bereich, in dem alle Punkte liegen, deren Abstand zu A kleiner ist als 4cm.

Lösung:
a) Sie liegen auf der Kreislinie.                  b)Diese Punkte liegen innerhalb des Kreises.

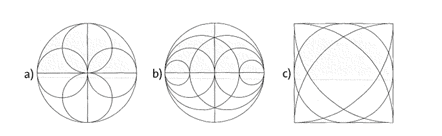
Übung 19 Zeichne die Kreismuster in dein Übungsheft (der Radius des großen Kreises beträgt 4 cm).

Übung 20 Vervollständige den Teddybär, indem du die fehlende Hälfte nach dem Vorbild mit Zirkel und Lineal konstruierst.

Übung 21 Zeichne in dein Übungsheft.

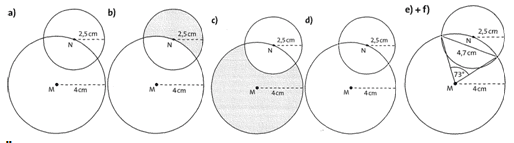
a) Markiere einen Punkt M und zeichne K(M; 4 cm). Markiere einen Punkt N auf der Kreislinie und zeichne den Kreis K(N; 2,5 cm).

b) Wo liegen alle Punkte, die von M mehr als 4 cm und von N weniger als 2,5 cm entfernt sind? Färbe den Bereich.

c) Wo liegen alle Punkte, die von N mehr als 2,5 cm und von M weniger als 4 cm entfernt sind? Färbe den Bereich.

d) Markiere die Punkte, die von M 4 cm und von N 2,5 cm entfernt sind.

e) Wie lang ist die zugehörige Sehne?

f) Miss den Mittelpunktswinkel zur Sehne aus e). Der zugehörige Scheitel sei M.

Lösung:

Übung 22 Wie können zwei Kreise mit unterschiedlichen Radien liegen, deren Kreislinien keine gemeinsamen Punkte haben? Skizziere alle Möglichkeiten und beschreibe die Lage der Kreise mit Worten.

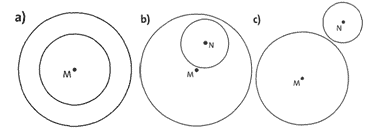
Lösung:
a) Ein Kreis kann im anderen liegen und beide haben denselben Mittelpunkt.
b) Ein Kreis kann im anderen liegen und beide haben unterschiedliche Mittelpunkte.
c) Sie können getrennt nebeneinander liegen.

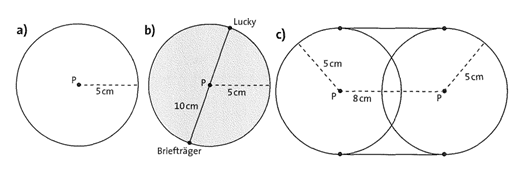
Übung 21 Der Hund Lucky ist an einer 5 m langen Leine an einem Pfahl P angebunden.

a) Zeichne in dein Übungsheft den Bereich, den ein Briefträger besser meiden sollte. Zeichne 1 cm für 1 m.

b) Der Briefträger gibt seinem Kollegen einen Tipp: „Wenn du den Hund liegen siehst, musst du von dieser Stelle nur mindestens fünf Meter Abstand halten, dann kann dir nichts passieren.” Hat er Recht? Wie groß muss der Mindestabstand sein? Tipp: Skizziere verschiedene Möglichkeiten.

c) Nun hat sein Herrchen für Lucky etwas Neues konstruiert: Die Leine endet in einem Ring, der an einer 8 Meter langen Stange entlang gleiten kann (siehe Abbildung). Zeichne den Bereich, in dem sich Lucky jetzt bewegen kann. Genügen nun 10 Meter Sicherheitsabstand von Luckys Aufenthaltsort?

Lösung:
b) Nein, das genügt nicht. Um ganz sicher zu gehen, muss man 10 m Abstand halten.
c) Man sollte 18 m Abstand halten.

WİSSEN

Umfang des Kreises – die Zahl π

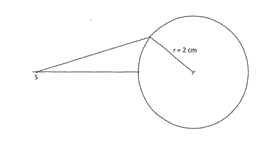
Übung 24 Eine Firma entwickelt ein neues elektrisches Spielzeug. Darin soll ein Elektromotor über ein Antriebsrad (eine kreisförmige Antriebsscheibe) den Schieber S bewegen.

a) Wie weit kann sich der Schieber maximal
hin- und her bewegen?

b) Das Antriebsrad soll mit Gummiummantelt werden. Wie
lang muss der Gummistreifen sein, der aufgeklebt wird?

Lösung:
a) Der Schieber kann maximal 4 cm bewegt werden, b) Der Gummistreifen muss 12,6 cm lang sein.