Nimmt man 2 Zahlen miteinander mal, so multipliziert man diese beiden Zahlen. Die Rechnung nennt man Multiplikation. Jede Multiplikation kann man als wieder-holte Addition von immer der gleichen Zahl auffassen.
So gilt also: 3 . 4- — 4 + 4 + 4 12

Häufig wird das Wort “Produkt” sowohl als Bezeichnung des Ausdrucks “3-3” als auch zur Bezeichnung seines Wertes “12” gebraucht.
Vorgehen beim schriftlichen Multpilizieren:
• Schreibe beide Faktoren nebeneinander.
• Multipliziere den 1. Faktor nacheinander mit allen Stellen des 2. Faktors.
• Ist der 2. Faktor mehrstellig, so wird er in Einer, Hunderter, Tausender, … zerlegt und berechnet. Anschließend werden alle untereinander geschriebenen Produkte addiert.
Beispeil :
1. Multipliziere schriftlich : 204.7
Lösungen :

2. Multipliziere schriftlich: 367.28

Lösungen : 

• Wenn du eine Zahl mit 1 multiplizierst, so entspricht das Produkt stets dieser Zahl.
• Wenn du eine Zahl mit 0 multiplizierst, so entspricht das Produkt stets 0.
• Wenn du eine Zahl mit 10, 1000, 1 000, … multiplizierst, so entspricht das Produkt stets dieser Zahl mit 1, 2, 3, … angehängten Nullen.
Beispeil :
a. 124.1 = 124 Multiplikation mit 1 lässt die Zahl unverändert.
b. 675.0 = 0 Multiplikation mit 0 ergibt immer 0.
c. 34.10 = 340 10 hat 1 Null -> Hänge 1 Null an die Zahl
d. 567.100 = 56 700 100 hat 2 Nullen -> Hänge 2 Nullen an
e. 8 093.1 000 = 8 093 000 1 000 hat 3 Nullen -> Hänge 3 Nullen an

55. Schreibe kürzer und berechne :
a) 8+8+8+8+8+8
b) 16+16+16
c) 1+1+1+1+1+1+1
d) 25+25+25+25
Lösungen : 
a) 6.8 = 48
b) 3.16 = 48
c) 7.1 = 7
d) 4.25 = 100
56. Schreibe jeweils als Summe mit lauter gleichen Summanden. (Es gibt verschiedene Möglichkeiten.)
a) 1.8
b) 27.2
c) 4.16
Lösungen : 
a) 1.8 = 1+1+1+1+1+1+1+1 8-mal der Summand 1
b) 27.2 = 2+2+2+2+2+2+2+2+2
2+2+2+2+2+2+2+2+2
2+2+2+2+2+2+2+2+2 27-mal der Summand 2
Oder 27.2 = 27+27
c) 4.16 = 16+16+16+16 4-mal der Summand 16
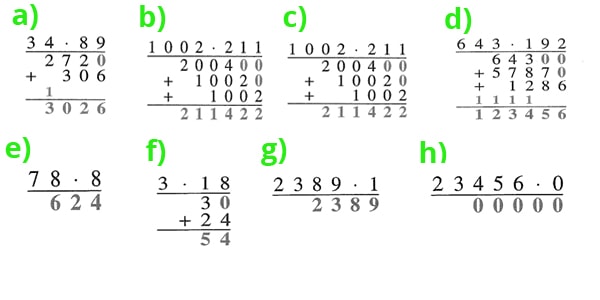
57. Berechne den Wert des Produkts schriftlich (falls nötig).
a) 34 . 89
b) 1 0002 . 211
c) 444 . 12 124
d) 643 . 192
e) 78 . 8
f) 3 . 18
g) 2 389 . 1
h) 23 456 . 0
57 Lösungen : 

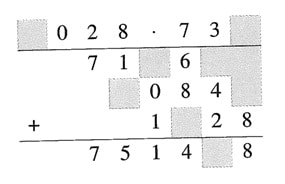
58. Fülle bei der folgenden schriftlichen Multiplikation die graunen Kästchen so, das Ergebnis stimmt.

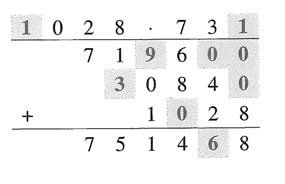
Lösungen 58 : 

59. Finde 3 verschiedene Zahlen (a,b,c) sodass gilt:
a) a.b.c=28
b) a.b.c=72
c) a.b.c=66

59 Lösungen
a) 1.4.7 = 28
b) 2.4.9 = 72
c) 2.3.11 = 66

60. Welche Aufgabe gehört zu welchem Ergebnis? Wenn du bei jeder Aufgabe vorher die Lösung überschlägst, kannst du viel Zeit sparen.
a) 34.79
b) 15.15
c) 49.21
d) 9.201
e) 154.95
f) 205.191
14 630 , 1 029, 225, 39 155, 1 809, 2 686

60 Lösungen
a) Überschlag : 34.79 ≈ 35.80 = 2 800
34.79 = 2 686
b) Überschlag : 15.15 ≈ 10.10 = 200 und 20.20 = 400
15.15 = 225
c) Überschlag : 29.21 ≈ 50.20 = 1000
49.21 = 1 029
d) Überschlag : 9.201 ≈ 10.200 = 2000
9.201 = 1 809
e) Überschlag : 154.95 ≈ 150.100 = 15 000
154.95 = 14 630
f) Überschlag : 205.191 ≈ 200.200 = 40 000
205.191 = 39 155

61. Bilde mit den ziffern
2, 3, 5
Alle möglichen Produkte mit 2 Faktoren und berechne sie. Jede Ziffer darf nur einmal vorkommen. Alle Umkehrungen sind erlaubt. (Wie viele mögliche Produkte gibt es?)
61 Lösungen : Diese Aufgabe kannst du nur durch geschicktes Kombinieren und Ausprobieren lösen. Im 9. Und 10. Schuljahr lernst du Methoden kennen, wie man die Anzahl der Möglichkeiten berechnet.
23.5=115 2.35=70 25.3=75
2.53=106 32.5=160 3.25=75
35.2=70 3.52=156 52.3=156
5.23=115 53.2=106 5.32=160
Mit den Umkehrungen gibt es 12 Möglichkeiten.