Parallelogramme
Ein Parallelogramm ist ein Viereck, bei dem gegenüberliegende Seiten jeweils parallel zueinander und gleich lang sind.
Achtung: Benachbarte Seiten steh

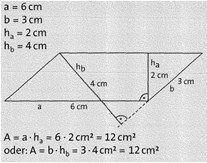
Der Abstand von zwei gegenüberliegenden Seiten heißt Höhe ha bzw. hb des Parallelogramms. Die Höhe kann auch außerhalb des Parallelogramms liegen.
Der Flächeninhalt eines Parallelogramms
ist das Produkt aus einer Seitenlänge und der zugehörigen Höhe.
Zwei Rechenwege sind möglich:
A = a • ha oder A = b – hb
Die beim Rechnen verwendete Seite heißt auch Grundseite g; die zugehörige Höhe heißt hg.
Man schreibt dann A = g • hg.
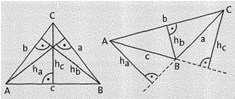
Dreiecke
Der Abstand eines Eckpunktes zur gegenüberliegenden Seite heißt eine Höhe des Dreiecks.
Jedes Dreieck besitzt drei Höhen ha, hb und hc. Diese können auch außerhalb des Dreiecks liegen.

Übung 12 Zeichne die Figuren auf ein Blatt Papier und schneide sie aus. Zerschneide jede der Figuren entlang der gestrichelten Linien und lege ihre Teile so zusammen, dass jeweils ein Rechteck entsteht. Miss die Seitenlangen der Rechtecke und berechne ihre Größe.
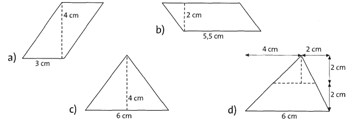
Lösung:
a) 12 cm2; b) 11 cm2; c) 12 cm2; d) 12 cm2
Übung 13 Erkläre anhand der Zerlegungen aus Übung 12…
a) warum man die Parallelogrammfläche mit der Formel „Grundseite mal Höhe” berechnen kann.
b) auch die Flächeninhaltsformel des Dreiecks.
Lösung:
a) Jedes beliebige Parallelogramm lässt sich auf diese (in 12 a) und b) gezeigte) Art zerlegen und zu einem Rechteck zusammensetzen,
b) Jedes beliebige Dreieck lässt sich auf diese (in 12 c) und d) gezeigte) Art zerlegen und zu einem Rechteck zusammensetzen.
Übung 14 Berechne die Flächeninhalte der abgebildeten Parallelogramme. Gib für jedes Parallelogramm die Länge der verwendeten Grundseite an!
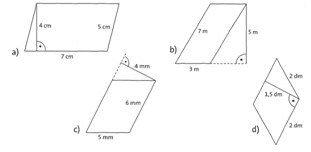
Lösung:
G = Grundseite a) 28 cm2, G = 7 cm; b) 15 m2, G = 3 m; c) 24 mm2, G = 6 mm; d) 3 dm2, G = 2 dm
Übung 15 Berechne die Flächeninhalte der Dreiecke. Bei dem rechtwinkligen Dreieck ist die Flächenberechnung besonders einfach.
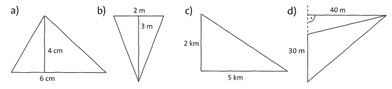
Lösung:
a) 12 cm2; b) 3 m2; c) 5 km2; d) 600 m2 = 6 a
Übung 16 Die fünf Figuren haben eine Seite gemeinsam. Welche hat die größte Fläche? Beantworte die Frage, ohne zu messen oder zu rechnen.
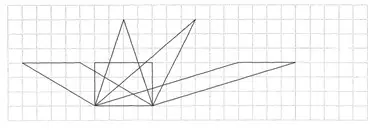
Lösung:
Die fünf Flächen sind alle gleich groß.
Übung 17 Zeichne fünf möglichst unterschiedlich aussehende Dreiecke mit dem Flächeninhalt
12 cm2. Überlege dir dazu, welche unterschiedlichen Kombinationen aus Grundseitenlänge und Höhe möglich sind.
Lösung:
Beispiele für mögliche Kombinationen (Grundseite x Höhe): 4 cm x 6 cm;
3 cm x 8 cm; 2 cm x 12 cm; 1cm x 24cm;
6 cm x 4 cm; 8 cm x 3 cm; 5 cm x 4,8 cm oder 10 cm x 2,4 cm.
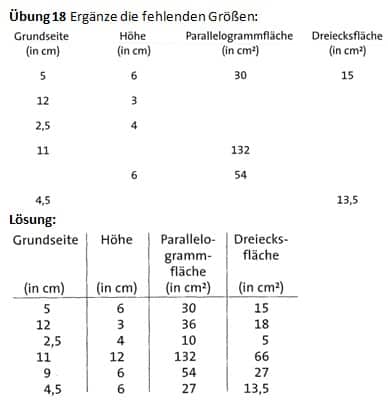
Übung 18 Ergänze die fehlenden Größen:
Übung 19 Löse die Aufgabe in einem Koordinatensystem. Zur Erinnerung: Der erste Wert gibt den Rechtswert, der zweite Wert den Hochwert eines Punktes an.
a) Zeichne das Dreieck A(1|2) B(5|2) C(7|6) in ein Koordinatensystem und zeichne die drei Höhen des Dreiecks ein. Verwende 2 Kästchen für eine Einheit!
b) Miss die Seitenlängen und die Höhen in Millimeter und trage die Werte ein.
c) Berechne den Flächeninhalt (in mm2) auf drei Arten, indem du jede Seite einmal als Grundseite verwendest.
d) Vergleiche die drei Ergebnisse miteinander. Stimmen sie genau überein? Woher kommen die Abweichungen?
Lösung:
b) a = 45 mm; b = 72 mm; c = 40 mm; ha = 36 mm; hb = 22 mm; hc = 40 mm

d) Die Abweichungen in den ersten beiden Rechnungen aus c) entstehen durch Ungenauigkeiten beim Messen. Das Dreieck hat den Flächeninhalt A = 800 mm2 = 8 cm2. (Die Werte in der dritten Rechnung aus c) sind exakt durch die Koordinaten von A, B und C vorgegeben.)
WİSSEN
Flächeninhalt von geradlinig begrenzten Figuren
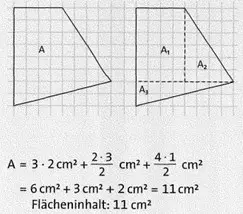
Den Flächeninhalt einer geradlinig begrenzten Figur kann man durch Zerlegen in Teilfiguren bestimmen:
Die Summe der Flächeninhalte der Teilfiguren ist gleich dem Flächeninhalt der Gesamtfigur.
Unterschiedliche Zerlegungen führen zu demselben Ergebnis.
Die entstandenen Teilflächen dürfen auch beliebig neu zusammengesetzt werden; der Flächeninhalt bleibt gleich.
Übung 20 Bestimme die Flächeninhalte der abgebildeten Figuren.
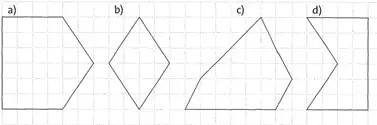
Lösung:
a) 7,5 cm2; b) 3 cm2; c) 6 cm2; d) 4,5 cm2
Übung 21 Berechne den Flächeninhalt des einbeschriebenen Parallelogramms, indem du die Größe der rechteckigen Fläche berechnest und davon die Inhalte der Dreiecksflächen abziehst.
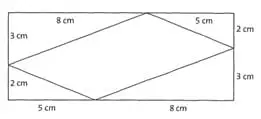
Lösung:
65 cm2 – 2-12 cm2 – 2-5 cm2 = 31 cm2
Übung 22 Eine Raute ist ein Parallelogramm mit vier gleich langen Seiten. Erkläre, warum man mit der unten stehenden Formel ihren Flächeninhalt berechnen kann.
A = (d, e Diagonalenlängen)
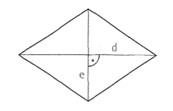
Lösung:
