Rationale Negative Zahlen

Wird der Zahlenstrahl nach links unendlich erweitert, erhält man die Zahlengerade. Die Zahlen links von der Null heißen negative Zahlen und werden durch ein negatives Vorzeichen (-) gekennzeichnet. Die Zahlen rechts von der Null heißen positive Zahlen, sie können durch ein positives Vorzeichen (+) gekennzeichnet werden.
Die Null ist weder positiv noch negativ.

Auch das Koordinatensystem (Achsenkreuz) kann in den negativen Bereich fortgesetzt werden.
Die Pfeilspitzen an den Achsen zeigen, in welche Richtung die Zahlen größer werden.

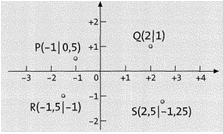
Betrag und Gegenzahl

Der Abstand einer Zahl zur Null heißt Betrag der Zahl. Haben zwei verschiedene Zahlen denselben Abstand zur Null, so heißt jede der beiden Zahlen die Gegenzahl (Spiegelzahl) der anderen.
Zwei Gegenzahlen liegen immer symmetrisch zum Nullpunkt.

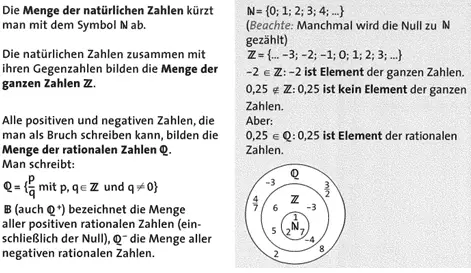
Zahlenmengen

Anordnung

Vergleichen von zwei Zahlen:
Liegt eine Zahl a auf der Zahlengeraden weiter links als eine Zahl b, so ist a kleiner als b.
Man schreibt: a < b.
Die Zahl b liegt dann weiter rechts als die Zahl a, also ist b größer als a.
Man schreibt daher auch: b > a.

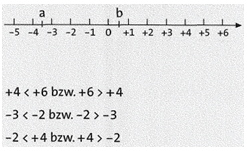
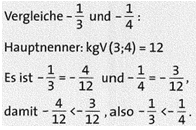
Bei gleichnamigen Brüchen werden die Zähler verglichen. Ungleichnamige Brüche werden zuerst gleichnamig gemacht (auf den Hauptnenner erweitert) und dann verglichen. (↑ Kap. 1.1)

Merke: Eine negative Zahl ist immer kleiner als eine positive Zahl!