Dezimalzahlen Addieren und Subtrahieren

Zur schriftlichen Addition werden die Dezimalzahlen stellenweise untereinander geschrieben: Ziffern mit gleichem Stellenwert stehen untereinander und Komma steht unter Komma. Dann wird, wie gewohnt, von rechts beginnend stellenweise addiert. Im Ergebnis wird das Komma stellengerecht genau unter denen der Rechnung eingefügt.

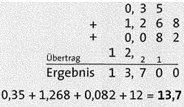
Zur schriftlichen Subtraktion werden die Dezimalzahlen stellenweise untereinander geschrieben: Ziffern mit gleichem Stellenwert stehen untereinander und Komma steht unter Komma. Dann wird, wie gewohnt, von rechts beginnend stellenweise subtrahiert. Im Ergebnis wird das Komma stellengerecht genau unter denen der Rechnung eingefügt.

Haben die Zahlen unterschiedlich viele Nachkommastellen, so kann man an die „kürzere“ Zahl Endnulien anhängen.

Dezimalzahlen Multiplizieren

Zur schriftlichen Multiplikation zweier Dezimalzahlen schreibt und rechnet man zunächst ohne Komma.
Das Ergebnis erhält genau so viele Dezimalen wie beide Faktoren zusammen. Endnullen des Ergebnisses werden bei der Kommasetzung mitgezählt. Geschrieben wird das Ergebnis ohne Endnullen. Beachte: Ist einer der Faktoren eine natürliche Zahl, so hat er null Dezimalen.

Bei der Multiplikation mit einer Zehnerpotenz (Stufenzahl) wird das Komma um so viele Stellen nach rechts gerückt, wie die Zehnerpotenz Nullen hat.

Dezimalzahlen Dividieren

Division einer Dezimalzahl durch eine natürliche Zahl: Man dividiert wie gewohnt. Im Ergebnis wird das Komma genau dann gesetzt, wenn man beim Dividieren das Komma überschreitet. Ist auch der Dividend eine natürliche Zahl, so denkt man sich das Komma nach den Einern geschrieben.

Ist der Dividend kleiner als der Divisor, so beginnt das Ergebnis mit „null Komma“. Gegebenenfalls entstehen nach dem Komma noch weitere Nullen.

Bei der Division einer Dezimalzahl durch eine Dezimalzahl verschiebt man in beiden Zahlen das Komma um dieselbe Anzahl von Stellen nach rechts, bis der Divisor eine natürliche Zahl ist. Dann wird eine Division durch eine natürliche Zahl ausgeführt. Der Wert des Quotienten ist derselbe wie der in der Ursprungsaufgabe.

Bei Division durch eine Zehnerpotenz wird das Komma im Dividenden um so viele Stellen nach links verschoben, wie die Zehnerpotenz Nullen hat.

Dezimalzahlen Runden

Interessiert nur die ungefähre Größe, so kann man eine Dezimalzahl auf eine vorgegebene Anzahl von Dezimalen runden. Es gelten folgende Regeln:
Ist die Dezimale nach der Rundungsstelle 0,1, 2, 3 oder 4, so wird abgerundet. Ist sie 5, 6, 7,8 oder 9, so wird aufgerundet.

Übung 12 Fülle die Lücken in den schriftlichen Rechnungen und ergänze die Ergebnisse.

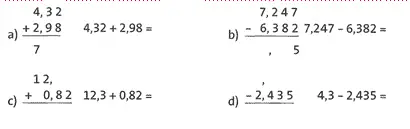
Lösung:
a) 7,3; b) 0,865; c) 13,12; d) 1,865

Übung 13 Hans führt eine Woche lang Buch über seine Einnahmen und seine Ausgaben. Ist er in dieser Woche reicher oder ärmer geworden?
Zu Wochenbeginn hatte er 10,50 €. Wie viel Geld hat er am Ende der Woche?

       Einnahmen                                                                             Ausgaben________
5,00 € Taschengeld                                                        2,30 € Computerzeitschrift
1,50 € abgegebene Pfandflaschen                          3,75 € Süßkram vom Bäcker
5,20€ Annas Schuldenrückzahlung                          2,99 € Geschenk für Salih
1,79 € Schlüsselanhänger

Lösung:
Hans ist reicher geworden. Er hat dann 11,37 €.

Übung 14 Fülle die Lücken in den Rechnungen aus. Setze anschließend jeweils das Komma an die richtige Stelle.

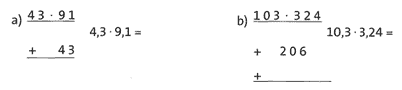
Lösung:
a) 39,13; b) 33,372

Übung 15 Berechne im Kopf und trage die Ergebnisse ein. Achte insbesondere bei der Multiplikation auf das Komma!
a) 2,2 + 2,1 =                      b) 7,2 + 0,6 =                    c) 5,3+ 5,8 =

d) 12,7 + 7,3 e) 2,2-2,1 = f) 18,3 – 5 =

g) 2,5 -1,3 = h) 6,2 – 3,8 = i) 2 • 1,3 =

j) 4 • 2,4 = k) 3,3 • 2 = I) 0,9 • 7 =

Lösung:
a) 4,3; b) 7,8; c) 11,1; d) 20; e) 0,1; f) 13,3 g) 1,2; h) 2,4; İ) 2,6; j) 9,6; k) 6,6; I) 6,3

Übung 16 Rechne schriftlich in deinem Übungsheft.

a) 2,23 + 7,78   b) 13,44 + 8,281   c) 12,05 + 0,055   d) 10,2 – 8,8

e) 3,15 – 1,48   f) 7,05-0,153   g) 1,95 . 3   h) 2,4 • 2,7

Lösung:
a) 10,01; b) 21,721; c) 12,105; d) 1,4; e) 1,67; f) 6,897; g) 5,85; h) 6,48

Übung 17 Fülle die Lücken in den Divisionen. Jedes leere Feld steht für eine Ziffer. Beim Ergebnis muss in eines der leeren Felder das Komma eingetragen werden.
Lösung:
a) 4,75; b) 0,84

Übung 18 Verschiebe in jedem der Terme das Komma zuerst so weit nach rechts, dass der Divisor eine natürliche Zahl ist. Führe dann eine Nebenrechnung durch und gib das Ergebnis an. Notiere auch, um wie viele Stellen du das Komma verschoben hast.

Lösung:
160 : 25 = 6,4 (um 1 Stelle)
1,705 : 55 = 0,031 (um 1 Stelle)
183 :12 = 15,25 (um 2 Stellen)
9720 : 2025 = 4,8 (um 3 Stellen)