Äquivalenzumformungen
Eine Gleichung liefert eine wahre Aussage, wenn auf beiden Seiten „gleich viel“ steht (wie bei einer Waage im Gleichgewicht). Man darf eine Gleichung in eine andere umformen, wenn Grundmenge und Lösungsmenge gleich bleiben.Solche Umformungen heißen Äquivalenzumformungen. Geschicktes Umformen einer Gleichung führt meist dazu, dass man die Lösung direkt ablesen kann.
Äquivalenzumformungen sind:
– Addieren oder Subtrahieren der gleichen Zahl (oder des gleichen Terms) auf beiden Seiten der Gleichung.
– Multiplizieren oder Dividieren beider Seiten der Gleichung mit einer von 0 verschiedenen Zahl (oder einem von 0 verschiedenen Term).
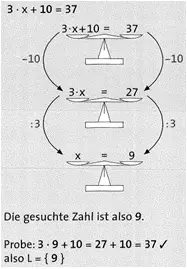
Lösen von Sachaufgaben
Stelle einen Term bzw. eine Gleichung mit Variablen (↑ Kap. 3.4) auf und bestimme die Lösungsmenge:
– Notiere alle Angaben aus der Aufgabenstellung, d.h. alle Größen, ihre Beziehung zueinander, und stelle fest, was gesucht wird.
– Fasse die Terme geschickt zusammen, bringe durch Äquivalenzumformungen die Variable auf die linke Seite des Gleichheitszeichens und die Zahlen auf die rechte Seite des Gleichheitszeichens.
Hinweis;
Statt 3 • x kannst du schreiben: 3x

Übung 1 Auf dem Bild siehst du eine Waage, in deren Waagschalen große und kleine Dosen gestapelt sind. Eine kleine Dose wiegt 100 g.
a) Bestimme durch geschicktes Wegstreichen das Gewicht einer großen Dose.
b) Stelle nun eine passende Gleichung auf, mit der du das Gewicht einer großen Dose berechnen kannst.
c) Bestimme (durch Äquivalenzumformungen) die Lösung der Gleichung und führe eine Probe durch.
d) Wie schwer wäre eine große Dose, wenn eine kleine Dose 150 g wiegen würde?
Lösung:
a) Eine große Dose wiegt so viel wie zwei kleine Dosen. Also wiegt eine große Dose 200 g.
b) 2 • d + 3 • 100 = 7 • 100
c) L = {200}
d) Eine große Dose wäre dann 300 g schwer.
Übung 2 Notiere jeweils rechts neben der Gleichung (hinter dem Strich |), welche Umformung auf der linken Seite durchgeführt wurde.
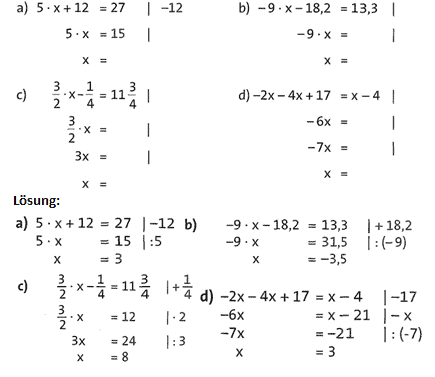
Übung 3 Löse folgende Gleichungen durch Äquivalenzumformungen, führe anschließend eine Probe durch. Schreibe in dein Übungsheft.
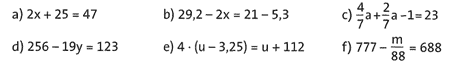
Lösung:
a) L = {11}; b) L = {6,75};
c) L = {28}; d) L = {7};
e) L = {41,6}; f) L = {7832}
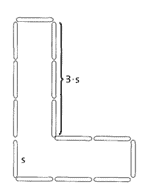
Übung 4 Eine Firma stellt Leuchtbuchstaben her.
a) Wie viele Leuchtstäbe s werden zur Herstellung des rechts
gezeigten Buchstabens L benötigt?
b) Schreibe – wie gezeigt – an den Buchstaben, wie viele Leuchtstäbe
pro Seite benötigt werden.
c) Gib als Term mit der Variablen s an, wie viele Leuchtstäbe insgesamt
benötigt werden – nutze die Ergebnisse aus b)!
d) Welchen Umfang hat ein solcher Buchstabe, wenn ein Leuchtstab 10 cm (20 cm, 14 cm) lang ist?
Lösung:
a) 14 Leuchtstäbe werden benötigt.
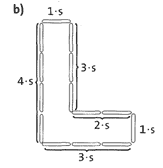
c) U = 14 • s
d) Wenn s = 10 cm, dann U = 140 cm. Wenn s = 20 cm, dann U = 280 cm. Wenn s = 14 cm, dann
U = 196 cm.
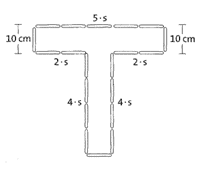
Übung 5 Dieselbe Firma wie in Übung 4 soll nun den rechts gezeigten Buchstaben T anfertigen. Die Länge der Leuchtstäbe steht noch nicht fest, es ist lediglich bekannt, dass der Querbalken 10 cm dick sein muss (siehe Skizze).
a) Welchen Umfang hat der Buchstabe, wenn s = 10 cm (20 cm)?
b) Gib einen Term mit der Variablen s an, mit dem man für
verschiedene Längen von s den Umfang schnell berechnen kann.
c) Berechne mit dem Term aus b) den Umfang für s = 14 cm
Lösung:
a) Wenn s = 10 cm, dann U = 200 cm. Wenn s = 20 cm, dann U = 380 cm.
b) U = 18 • s + 20 Wenn s = 14 cm, dann U = 272 cm.
a) Er muss 10 ct pro Ei verlangen.
b) Er muss 12 ct pro Ei verlangen.
c) Er muss 15 ct pro Ei verlangen.
Übung 8 Gegeben ist die Gleichung 3 • (4 + x) = 14 + 3x – 2.
a) Setze verschiedene Zahlen aus Q für x ein. Was stellst du fest?
b) Überlege dir, wann eine Zahl eine Lösung einer Gleichung ist (↑ Kap. 3.5).Was kannst du also über die Zahlen sagen, die du eingesetzt hast?
c) Vereinfache beide Seiten der Gleichung so weit wie möglich. Was stellst du fest?
Lösung:
a) Die Gleichung liefert für alle aus Q eine wahre Aussage.
b) Alle eingesetzten Zahlen sind Lösungen der Gleichung.
c) Die Vereinfachung ergibt: 12 + 3x = 12 + 3x. Die Terme auf beiden Seiten der Gleichung sind gleichwertig.
Übung 9 Finde heraus, welche Zahl man für x einsetzen muss, um eine wahre Aussage zu erhalten. Schreibe jeweils rechts neben die Gleichung, welche Umformung auf beiden Seiten durchgeführt wurde, um die Gleichung der nächsten Zeile zu erhalten.
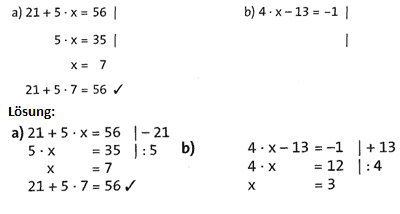
WİSSEN
Äquivalente Terme und Lösungsmengen
Nehmen zwei Terme immer denselben Wert an, egal welche Zahl (aus der Grundmenge) man einsetzt, so sind sie äquivalent (lateinisch gleichwertig).

Wendet man die Rechengesetze bei der Termumformung richtig an, so erhält man immer einen äquivalenten Term.

Wenn eine Gleichung für jede Belegung der Variablen durch eine beliebige Zahl aus der Grundmenge eine wahre Aussage liefert, nennt man sie allgemein gültig. Ist die Grundmenge einer solchen Gleichung Q, so ist die Lösungsmenge ebenfalls Q. Äquivalenzumformungen führen zu einer wahren Aussage, bei der die Variable keine Rolle mehr spielt.

Eine Gleichung, die für keine Zahl aus der Grundmenge eine wahre Aussage liefert, heißt nicht lösbar (nicht erfüllbar). Äquivalenzumformungen einer solchen Gleichung führen zu einer falschen Aussage. Die Lösungsmenge ist die leere Menge.
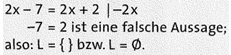
Übung 10 Bestimme die Lösungsmengen (Grundmenge = Q) der folgenden Gleichungen:
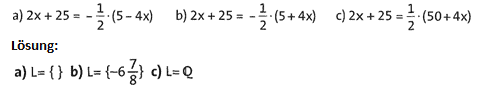
Übung 11 Christina surft gerne im Internet. Sie hat einen Vertrag abgeschlossen, bei dem zu einer monatlichen Grundgebühr in Höhe von 5,50 € Verbindungskosten in Höhe von 6 Cent pro Minute kommen.
a) Wie viel muss Christina zahlen, wenn sie 4 Stunden und 44 Minuten im Internet war?
b) Im folgenden Monat zahlt sie 31,30 €. Wie lange war sie im Internet?
c) Timo hat einen Vertrag, bei dem er pauschal 35 € im Monat zahlt – egal, wie lange er im Internet ist. Im ersten Monat waren es 6 Stunden und 40 Minuten, im zweiten Monat 4 Stunden und 30 Minuten. Lohnt sich dieser Vertrag oder wäre Christinas Vertrag besser geeignet?
Lösung:
a) Sie muss 22,54 € zahlen, wenn sie 4 Stunden und 44 Minuten im Internet war.
b) Sie war 430 Minuten im Internet.
c) Timo würde mit Christinas Vertrag im 1. Monat 29,50 €, im 2. Monat 21,70 € zahlen, also wäre ihr Vertrag besser geeignet.