Wandle nun Brüche in Dezimalzahlen um. Dividiere schriftlich den Zähler durch den Nenner des Bruches.

Übung 6
Wandle in eine Dezimalzahl um.

Lösung:
a) 1,5                    b) 40,0                  c) 4,25                  d) 0,01                  e) 3,333…

Bei der Umwandlung des letzten Bruches hast du bemerkt, dass bei der Division von 10 durch 3 fortlaufend der Rest 1 bleibt. Nach dem Komma ergeben sich unendlich viele Dreien. Die Dezimalzahl 3,333… ist eine einfach periodische Dezimalzahl.
Wir schreiben: 3,3.
Der Strich über der 3 nach dem Komma gibt an, dass sich diese Ziffer unendlich oft (periodisch) wiederholt.
Lies «drei Komma Periode drei».

Es gibt auch periodische Dezimalzahlen, deren Periode aus mehreren Ziffern besteht.

Biespiel

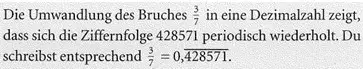
Diese Dezimalzahl heißt 6fach periodisch. Unter dem Periodenstrich stehen sechs Ziffern.

Übung 7
Wandle in Dezimalzahlen um. Gib die Periode an.

Im Beispiel und in den Übungen beginnt die Periode sofort nach dem Komma. Das muss nicht immer so sein.

Lösung:

Biespiel

1,16 ist eine nicht sofort periodische Dezimalzahl. Lies «eins Komma eins Periode sechs». Zahlen wie 3,3 oder 0,428571 heißen im Gegensatz dazu sofort periodische Dezimalzahlen.

Übung 8
Wandle in Dezimalzahlen um. Gib an, ob diese sofort oder nicht sofort periodisch sind.

Lösung:

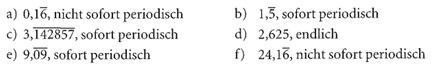
Du kannst jeden Bruch mit Hilfe der schriftlichen Division in eine Dezimalzahl umwandeln. Diese Dezimalzahl kann endlich sein (z. B. 8,5). Sie kann aber auch unendlich, d. h. periodisch sein (z. B. 8,5). Die Periode besteht entweder aus einer einstelligen oder aus einer mehrstelligen natürlichen Zahl. Die zugehörige Dezimalzahl ist dann einfach oder mehrfach periodisch. Die Periode kann an einer beliebigen Stelle nach dem Komma beginnen.