Zehnersystem und große zahlen 5. klasse

Die heutigen Zahlzeichen stammen aus Arabien. Seit ungefähr 500 Jahren ver-wendet man diese Zeichen in Europa. Schon frühzeitig haben die Araber beim Schreiben von Zahlen Zehnerbündel gebildet und verwendet. Dieses System der Schreibweise von Zahlen heißt Zehnersystem oder Dezimal-system (lat: decem= zehn). Die Schreibweise des Zehnersystems hat also ihren Ursprung in der Zahl 10. Diese Zahl 10 findest du in deinen zehn Fingern wieder; das heißt: Die Finger waren der Ausgangspunkt des Dezimalsystems.

# Das Dezimalsystem (Zehnersystem) ist ein Stellenwertsystem, da es von der Stelle innerhalb einer Zahl abhängt, welchen Wert eine Zieffer hat Somit kann die gleiche Ziffer verschiedene Stellenwerte einnehmen.
# Die Zahlen 0, 1, 2, 3, 4, 5, … bezeichnet man als die Menge der natürlichen Zahlen, in Mengenschreibweise N = {0, 1, 2, 3, 4, 5, …}
# Die Zahlen 1, 10, 100, 1000, 10.000, … bezeichnet man als Zehnerzahlen.

Hinweis : In manchen Schulbüczern zählt die 0 nicht zu den natürlichen Zahlen!

Beispiele 1: Jede 5 in der Zahl 5 555 hat einen anderen Stellenwert:
Die letzte 5 steht für 5 Einer, die zweitlezte steht für 5 Zehner, die
Drittletzte für 5 Hunderter und die erste 5 steht für 5 Tausender.
Beispiele 2: Das Stellenwertsystem zeigt die Bündelung im Zehnersystem:

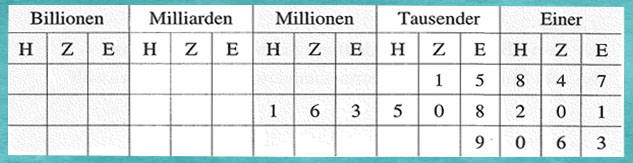
Folgende Zahlen sind dargestellt:
15 847 = 1 . 10 000 und 5 . 1 000 und 8 . 100 und 4 . 10 und 7 . 1
163 508 201 = 1 100 000 000 und 6 . 10 000 000 und 3 . 1 000 000 und
5 . 100 000 und 0 . 10 000 und 8 . 1 000 und 2 . 100 und
0 . 10 und 1 . 1
9 063 = 9 . 1 000 und 0 . 100 und 6 . 10 und 3 . 1
Jede natürliche Zahl hat einen Vorgänger (V) und einen Nachfolger (N). Eine Ausnahme bildet die Zahl 0, sie hat keinen Vorgänger.
Beispiel 1: Nenne Vorgänger (V) und Nachfolger (N) von :
a) 5 402 200
b) 199 999 999
Lösung 1 :
a) (V) : 5 402 199 (N) : 5 402 201
b) (V) : 199 999 998 (N) : 200 000 000
Große Zahlen und ihre Bezeichnungen
3 Nullen -> Tausend
6 Nullen -> Millionen
9 Nullen -> Milliarden
12 Nullen -> Billionen
15 Nullen -> Billiarden
18 Nullen -> Trillionen
21 Nullen -> Trilliarden
24 Nullen -> Quadrillionen
27 Nullen -> Quadrilliarden
30 Nullen -> Quintillionen
Große Zahlen sind leichter zu lesen, wenn sie in Dreierblöcke eingeteilt werden:
Statt 34560078 schreibt man 34.560.078 oder 34 560 078.
In Worten geschriebene Zahlen schreibt man klein und zusammen, wenn sie unter 1 Million liegen. Liegen Zahlen über 1 Million, schreibt man sie getrennt.

Zahlenstrahl Und Anordnung der natürlichen Zahlen Beispiele

Beispiel : Schreibe in Worten;
a) 2 405 801
b) 8 129 000 012
Lösung :
a) zwei Millionen vierhundertfünftausendachthunderteins
b) acht Milliarden einhundertneunundzwanzig Millionen zwölf

Beispiel 1 : Nenne Zahlen, die
a) 10-mal
b) 100-mal
c) 1 000-mal
so groß sind wie 603, 34 001 und 1 441.

Lösung 1 :

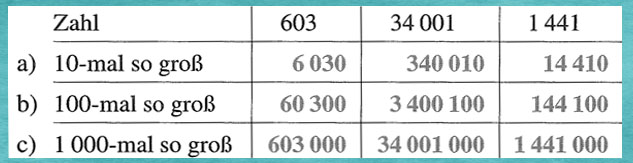
Um 10-mal, 100-mal oder 1.000 mal so große zahlen zu bekommen, fügt einmal eine 0, zweimal eine 0 oder dreimal eine 0 an.
Beispiel 2: Ordne die folgenden Zahlendarstellungen zuerst der Größe nach von der größten Zehnerzahl absteigend bis zur kleinsten Zehnerzahl und ergänze dabei auch die fehlenden Zehnerzahlen. Ermittle danach die Zahl im Dezimalsystem.
Beispiel a) 9.1 +9. 1 000 + 9 . 10 000
Lösung a) 9.10 000 + 9.1 000 + 0.100+0.10+9.1 = 00 009
Beispiel b) 7.1000+4 – 10+0.100+0.1
Lösung b) 7.1 000+0.100+4.10+0.1=7 040
Beispiel c) 4.100+4.100 000
Lösung c) 4. 100 000+0.10 000 + 0.1 000+4.100+0.10+0.1=400 400
Beispiel d) 6.100+8.10 000 + 1.10 + 3.1 000
Lösung d) 8.10 000+3.1 000+6.100+1.10+0.1=83 610

Beispiel 3: In Lexika findest du viele Zahlenangaben (Statistiken). Zum Beispiel:
• Der größte Staat der Erde heißt Russland und hat eine Fläche von 17 075 400 km2.
• Der bevölkerungsreichste Staat der Erde heißt Volksrepublik China und hat .1 322 000 000 Einwohner.
• Die Bundesrepublik Deutschland hat eine Fläche von 357 092 km2.
• Der Mensch hat ungefähr hundert Milliarden Gehirnzellen.
• Vor ungefähr fünfhundert Millionen Jahren tauchten auf der Erde die ersten Fische auf.
Trage diese Zahlendaten in die Stellenwerttafel ein und benenne die Zahlen

Lösungen

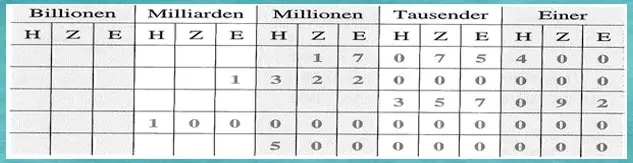
17 075 400 km2= siebzehn Millionen fünfundsiebzigtausendvierhundert km2
1 322 000 000 Einwohner = eine Milliarde dreihundertzweiundzwanzig Millionen Einwohner
357 092 km2 = dreihundertsiebenundfünfzigtausendzweiundneunzig km2
100 000 000 000 Gehirnzellen = einhundert Milliarden Gehirnzellen
500 000 000 Jahre — fünfhundert Millionen Jahre

Beispiel 4: Schreibe in Ziffern:
Trage die Zahlen „in Gedanken” in eine Stellenwerttafel ein und ergänze die fehlenden Nullen. Falls dir dies zu schwerfällt, zeichne zuvor eine Stellenwerttafel und trage dann ein.
Trilliarden – Trillionen – Billiarden – Billionen – Milliarden – Millionen – Tausender – Einer
a) elf Milliarden = 11 000 000 000 9 Nullen
b) dreizehn Trillionen = 13 000 000 000 000 000 000 18 Nullen
c) hunderteins Billionen = 101 000 000 000 000 12 Nullen
d) zwei Trilliarden einhundert Trillionen = 2 100 000 000 000 000 000 000 20 Nullen
Beispiel 5: Wie viele Nullen hat die Zahl
Trage die Zahlen ebenfalls „in Gedanken” in eine Stellenwerttafel ein, ergänze die fehlenden Nullen und zähle anschließend ab. Falls dir dies zu schwerfällt, zeichne zuvor eine Stellenwerttafel und trage dann ein.
a) zwanzig Milliarden = Hat 10 Nullen 20 000 000 000
b) achtunddreißig Billionen = Hat 12 Nullen 38 000 000 000 000
c) einhundert Millionen = Hat 8 Nullen 100 000 000
d) zwanzig Billiarden = Hat 16 Nullen 20 000 000 000 000 000

Beispiel 6: Nenne Vorgänger und Nachfolger folgender Zahlen

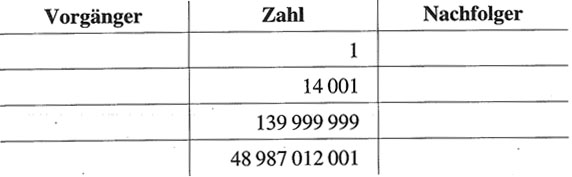
Vorgänger ist die direkt vorausgehende Zahl, Nachfolger ist die direkt nachfolgende Zahl.

Lösungen:

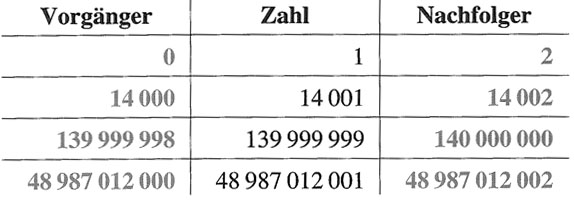
Beispiel 7: Nenne die größte und kleinste 6-ziffrige Zahl.
Lösungen 7:
Größte 6-ziffrige Zahl : 999 999
Kleinste 6-ziffrige Zahl : 100 000
Beispiel 8: Familie Ballschuh kauft eine neue Küche für 6 300 €. Sie bezahlen bar und haben nur 500-€-Scheine und 100-€-scheine.
Wie könnten sie bezahlen? Finde 5 Möglichkeiten.

Lösungen 8:
Es gibt natürlich noch viele andere Möglichkeiten, zu bezahlen. Für jeden 500-€-Schein weniger, muss man fünf weitere 100-€-Scheine bereithalten.
5 mögliche Bezahlmöglichkeiten für 6 300 €:
12 x 500-€–Scheine und 3 x 100-€-Scheine
11 x 500-€-Scheine und 8 x 100-€-Scheine
10 x 500-€-Scheine und 13 x 100-€-Scheine
9 x 500-€-Scheine und 18 x 100-€-Scheine
8 x 500-€–Scheine und 23 x 100-€-Scheine
Beispiel 9:

a) Bilde aus den 4 unten stehenden Zahlen durch Hintereinanderlegen die kleinste und die größte 6-steilige Zahl.
Lösungen: Kleinste Zahl: 1-14-18-3 also 114 183
Größte Zahl: 3-18-14-1 also 318 141
b) Bilde aus den 4 unten stehenden Zahlen eine Zahl, die möglichst nahe an 130 000 liegt.
3 14 1 18

Lösungen 1-3-14-18 also 131 418 liegt am nächsten bei 130 000.
Die Differenz zu 130 000 ist mit 131 418 – 130 000 = 1 418am kleinsten.

Anordnung der natürlichen und der ganzen Zahlen

Erweitert man die Menge der natürlichen Zahlen. N={0;1;2;3;…} um die negativen Zahlen, erhält man die Menge der ganzen Zahlen Z={…; -3; -2; -1; 0; 1; 2; 3; …}. Die natürlichen und die ganzen Zahlen lassen sich der Größe nach ordnen. Der Vorgänger einer Zahl ist um 1 kleiner, der Nachfolger um 1 größer als die Zahl selbst. Der Abstand einer Zahl zur Null heißt Betrag der Zahl. Haben zwei verschiedene ganze Zahlen denselben Abstand zur Null, so heißt jede der beiden Zahlen Gegenzahl der anderen.

Beispiel :
1. Trage die fehlenden Zahlen Ein.

Lösungen: Zahlengerade von links : -250; -150; -75; -25; 50; 100

2. Wie heißt die Gegenzahl und wie groß ist der Betrag beider Zahlen? Wie heißt der Vorgänger?

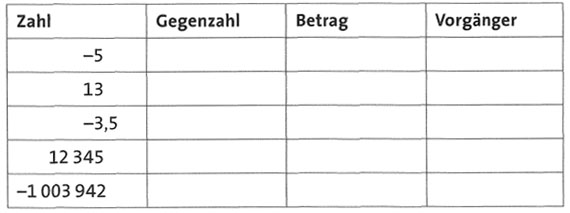
Lösungen :

Große Zahlen

Um auch große Zahlen einfach benennen zu können, werden immer 1000 Einheiten zu einer nächsthöheren Eihheit mit einem neuen Zahlwort zusammengefasst:
1 000 =1 Tausend
1 000 000 = 1 Million
1 000 000 000 =1 Milliarde
1 000 000 000 000 = 1 Billion
Zur besseren Übersichtlichkeit kann man große Zahlen durch Zwischenräume in Dreierpäckchen gliedern.
3. Lies die folgenden Zahlen und schreibe ihre Zahlwörter.
a) 1 302 405 116 – eine Milliarde dreihundertzwei Millionen vierhundertfünftausendeinhundertsechzehn
b) 52 546 987 – zweiundfünfzig Millionen fünfhundertsechsundvierzigtausendneunhundertsiebenundachtzig
c) 770 001 234 955 – siebenhundertsiebzig Milliarden eine Million zweihundertvierunddreißigtausend neunhundertfünfundfünfzig
4. Schreibe mit Ziffern.
a) achthundertsechsunddreißig Milliarden neunhundertvierundachtzig Millionen fünftausendzweiundvierzig – 836 984 005 042
b) fünfzehn Milliarden neunhundertsechsundsechzigtausendelf – 15 000 966 011
c) vierhundertzweiundsiebzig Billionen eintausendzwölf – 472 000 000 001 012
5. Schreibe als Zahl und in Worten.
a) Eine 7-stellige Zahl, in der keine Ziffer außer der 3 workommt.
a) 3 333 333 = drei Millionen dreihundertdreiunddreißigtausend dreihundertdreiunddreißig

b) Eine 12-stellige Zahl, die vorne sechsmal die Ziffer 4 und am Ende sechsmal die Ziffer 9 enthält.
b) 444 444 999 999 = vierhundertvierundvierzig Milliarden vierhundertvierundvierzig Millionen neunhundertneunundneunzigtausend neunhundertneunundneunzig

c) Die kleinstmögliche 9-stellige Zahl, die alle geraden Ziffern enthält; dabei soll die Zahl weder die Null nochungerade Ziffern enthalten.
c) 222 222 468 = zweihundertzweiundzwanzig Millionen zweihundertzweiundzwanzigtausend vierhundertachtundsechzig

d) An der 11. Stelle steht eine 2, an der 12. Eine 5, sonst besteht die Zahl nur aus Nullen.
d) 520 000 000 000 = fünfhundertzwanzig Milliarden